11.2 Correction for light curvature
A further complication arises, however, from the fact that light (or any other radiation) does not travel in a straight line through the earths atmosphere. This is because the refractive index of the atmosphere reduces with height, making it act like a giant lens. To see the effect of this, first consider what happens when part of a wave front of light travels from a medium with refractive index n1 to one with (lower) refractive index n2, as shown in Figure 11.3. During the time that the left end of the wave front travels from A to A², the right end (which is still in the denser medium) only travels from B to B². Thus the wave front changes from making an angle a with the interface to making an angle b with it, where a and b are related by the equation:
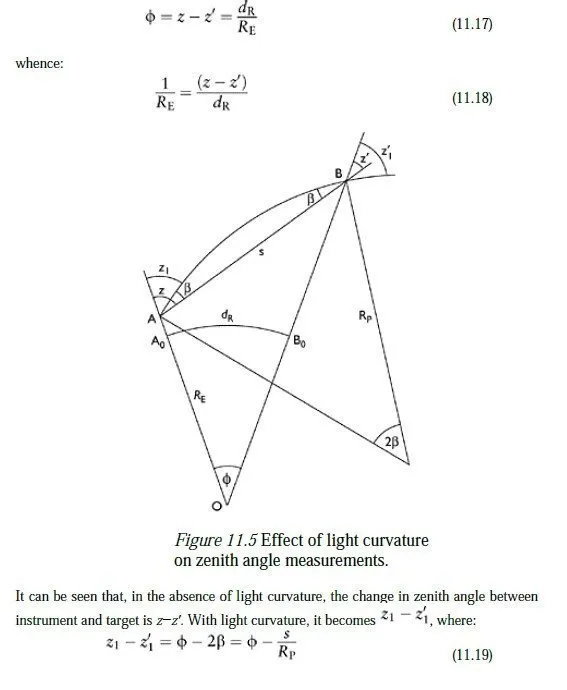
where RP is the radius of curvature of light which is travelling at a zenith angle z through the atmosphere. Conveniently, it turns out that the quantity (1/n)(dn/dh), which is a property of the atmosphere, is more or less constant throughout the atmosphere, for a given wavelength of light. It is also negative, which means that the light tends to curve towards the earth as shown in Figure 11.4. The actual light path in Figure 11.2 is therefore not a straight line as shown, but a curved line bulging above the straight line joining the instrument and target. The geometry of Figure 11.2 can be used, however, if one imagines a distortion of the picture in which the left edge of the picture is rotated clockwise and the right edge is rotated anticlockwise, so that the curved light path is bent back to become a straight line. The effect of this distortion would be to make the vertical lines through the instrument and target intersect further down the paper, i.e. to increase RE. It turns out that the effect of light curvature can be allowed for in exactly this way, by using an effective earth radius which is slightly larger than its actual radius. The mathematical derivation of this effective radius is given below. Figure 11.5 shows the effect of light curvature on the geometry of Figure 11.2, again greatly exaggerated; the light is assumed to have constant curvature of radius Rp, based on the mean zenith angle of the light path. We can write:
Letting R1 represent the effective earth radius described above, we can therefore write
the equivalent of equation 11.18, namely: