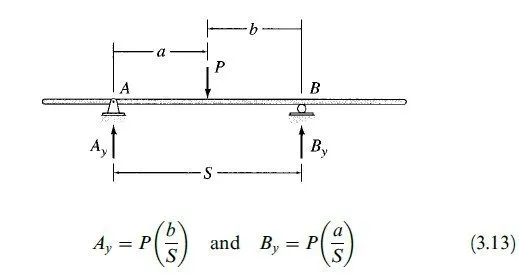
Consider a simply supported beam subjected to a vertical concentrated load P, as shown in Fig. 3.26. By applying the moment equilibrium equations, ∑MB =0 and ∑MA =0, we obtain the expressions for the vertical reactions at supports A and B, respectively, as

where, as shown in Fig. 3.26, a = distance of the load P from support A (measured positive to the right); b ¼ distance of P from support B (measured positive to the left); and S ¼ distance between supports A and B. The first of the two expressions in Eq. (3.13) indicates that the magnitude of the vertical reaction at A is equal to the magnitude of the load P times the ratio of the distance of P from support B to the distance between the supports A and B. Similarly, the second expression in Eq. (3.13) states that the magnitude of the vertical reaction at B is equal to the magnitude of P times the ratio of the distance of P from A to the distance between A and B. These expressions involving proportions, when used in conjunction with the principle of superposition, make it very convenient to determine reactions of simply supported structures subjected to series of concentrated loads, as illustrated by the following example.

Example 3.12

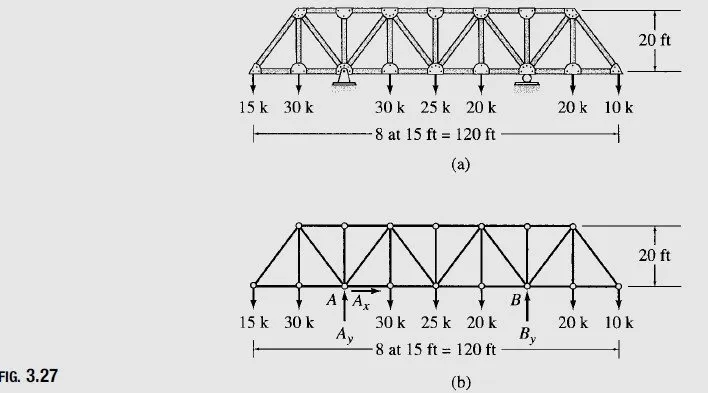
Determine the reactions at the supports for the truss shown in Fig. 3.27(a).

Solution
Free-Body Diagram See Fig. 3.27(b).
Static Determinacy The truss is internally stable with r =3. Therefore, it is statically determinate.
Support Reactions

+ -> �?Fx = 0
Ax = 0