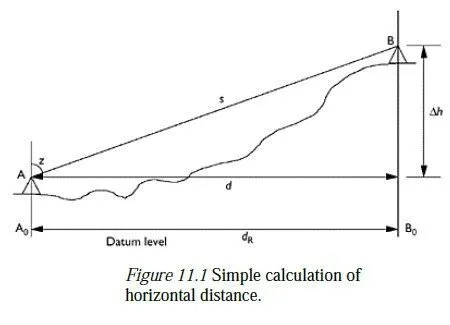
The reduction of distance measurements means the process of converting a measured slope distance between two points to the reduced distance over the ellipsoid between the projections of the two points onto the ellipsoid. It is useful to start by thinking of the simple geometry which would arise if the earth were flat, as shown in Figure 11.1. The quantities which would be measured are the zenith angle z and the slope distance s. It is clear that we can then write:

To a first approximation, these quantities will always be correct, even when the curvature of the earth is considered, but they are not sufficiently accurate to be used directly in surveying calculations.

11.1 Correction for the earths curvature

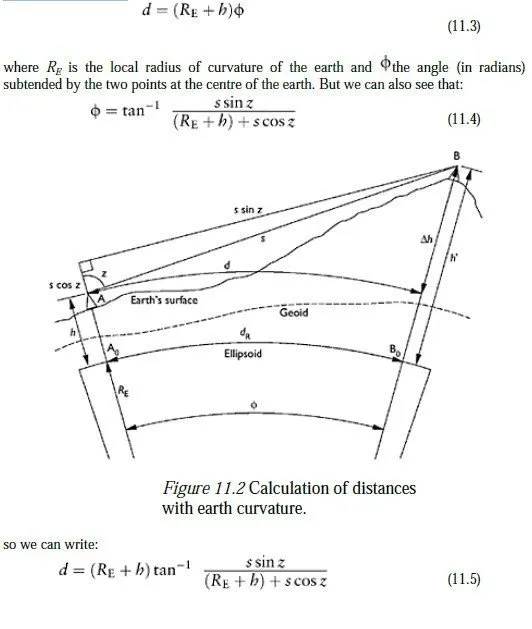
Although the earth is not perfectly spherical, the imperfection is in fact extremely small; its diameter at the equator is only about 0.3 per cent greater than the distance between the North and South Pole. For the purposes of distance calculations on the surface of the earth, it is therefore perfectly acceptable to assume that the earth is a sphere; the mean radius is usually assumed to be 6.38×106 m. The effect of the curvature of the earth is shown (greatly exaggerated) in Figure 11.2. Here we can see that:

For all realistic combinations of h, s and z, it turns out that the error in calculating d is less than one part per million if h is simply assumed to be zero in equation 11.5. It therefore becomes possible for a total station or other EDM device to calculate the horizontal distance between two stations to a high degree of accuracy, given a built-in average value for RE and no information about the height of either station. When the value of h is known, this distance can subsequently be converted to the reduced distance dR, using the simple formula:

As with equation 11.5, this equation still gives a highly accurate estimate for the vertical distance between two stations if h is simply assumed to be zero; for distances of up to 20 km, the resulting error in the value of Δh will be less than one millionth of the measured slope distance.