Alternative Approach An alternative approach that can be used for determining the static instability, determinacy, and indeterminacy of internally unstable structures is as follows:
1. Count the total number of support reactions, r.
2. Count the total number of internal forces, fi, that can be transmitted through the internal hinges and the internal rollers of the structure.
Recall that an internal hinge can transmit two force components, and an internal roller can transmit one force component.
3. Determine the total number of unknowns, r þ fi.
4. Count the number of rigid members or portions, nr, contained in the structure.
5. Because each of the individual rigid portions or members of the structure must be in equilibrium under the action of applied loads, reactions, and/or internal forces, each member must satisfy the three equations of equilibrium (∑Fx = 0, ∑Fy = 0, and ∑M = 0). Thus, the total number of equations available for the entire structure is 3nr. 6. Determine whether the structure is statically unstable, determinate, or indeterminate by comparing the total number of unknowns, r + fiy, to the total number of equations. If
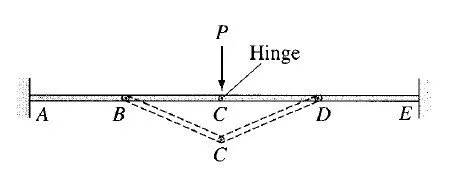
therefore, according to Eq. (3.9), the beam is supported by a su°cient number of reactions, and it should be statically determinate. However, it can be seen from the figure that portion BCD of the beam is unstable because it cannot support the vertical load P applied to it in its undeformed position. Members BC and CD must undergo finite rotations to develop any resistance to the applied load. Such a type of geometric instability can be avoided by externally supporting any portion of the structure that contains three or more internal hinges that are collinear.