Internal Stability
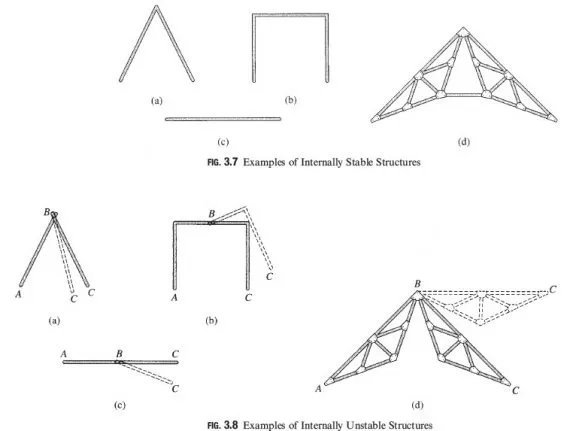
A structure is considered to be internally stable, or rigid, if it maintains its shape and remains a rigid body when detached from the supports. Conversely, a structure is termed internally unstable (or nonrigid) if it cannot maintain its shape and may undergo large displacements under small disturbances when not supported externally. Some examples of internally stable structures are shown in Fig. 3.7. Note that each of the structures shown forms a rigid body, and each can maintain its shape under loads. Figure 3.8 shows some examples of internally unstable structures. A careful look at these structures indicates that each structure is composed of two rigid parts, AB and BC, connected by a hinged joint B, which cannot prevent the rotation of one part with respect to the other.
should be realized that all physical bodies deform when subjected to loads; the deformations in most engineering structures under service conditions are so small that their e¤ect on the equilibrium state of the structure can be neglected. The term rigid structure as used here implies that the structure o¤ers significant resistance to its change of shape,
whereas a nonrigid structure o¤ers negligible resistance to its change of shape when detached from the supports and would often collapse under its own weight when not supported externally.
Static Determinacy of Internally Stable Structures
An internally stable structure is considered to be statically determinate externally if all its support reactions can be determined by solving the equations of equilibrium. Since a plane internally stable structure can be treated as a plane rigid body, in order for it to be in equilibrium under a general system of coplanar loads, it must be supported by at least three reactions that satisfy the three equations of equilibrium (Eqs. 3.2, 3.3, or 3.4). Also, since there are only three equilibrium equations, they cannot
be used to determine more than three reactions. Thus, a plane structure that is statically determinate externally must be supported by exactly three reactions. Some examples of externally statically determinate plane structures are shown in Fig. 3.9. It should be noted that each of these structures is supported by three reactions that can be determined by solving the three equilibrium equations.
be used to determine more than three reactions. Thus, a plane structure that is statically determinate externally must be supported by exactly three reactions. Some examples of externally statically determinate plane structures are shown in Fig. 3.9. It should be noted that each of these structures is supported by three reactions that can be determined by solving the three equilibrium equations.