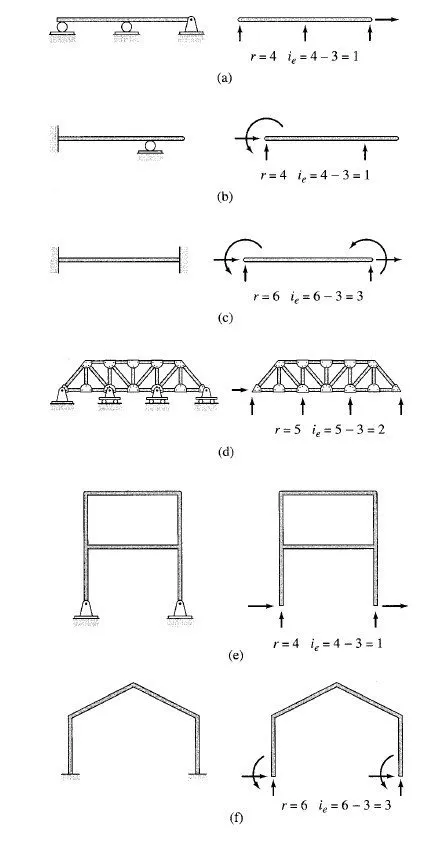
If a structure is supported by more than three reactions, then all the reactions cannot be determined from the three equations of equilibrium. Such structures are termed statically indeterminate externally. The reactions in excess of those necessary for equilibrium are called external redundants, and the number of external redundants is referred to as the degree of external indeterminacy. Thus, if a structure has r reactions r > 3, then the degree of external indeterminacy can be written as
Figure 3.10 shows some examples of externally statically indeterminate plane structures. If a structure is supported by fewer than three support reactions, the reactions are not su°cient to prevent all possible movements of the structure in its plane. Such a structure cannot remain in equilibrium under a general system of loads and is, therefore, referred to as statically unstable externally. An ex
ample of such a structure is shown in Fig. 3.11. The truss shown in this figure is supported on only two rollers. It should be obvious that although the two reactions can prevent the truss from rotating and translating in the vertical direction, they cannot prevent its translation in the horizontal direction. Thus, the truss is not fully constrained and is statically unstable. The conditions of static instability, determinacy, and indeterminacy of plane internally stable structures can be summarized as follows:
where r = number of reactions.
It should be realized that the first of three conditions stated in Eq. (3.8) is both necessary and su°cient in the sense that if r < 3, the structure is definitely unstable. However, the remaining two conditions, r =3 and r > 3, although necessary, are not succient for static determinacy and indeterminacy, respectively. In other words, a structure may be supported by a su°cient number of reactions r=>3 but may still be unstable due to improper arrangement of supports. Such structures are