The definition of continuous composite beam given in Eurocode 4: Part 1.1[12] is: A beam with three or more supports, in which the steel section is either continuous over internal supports or is jointed by full strength and rigid connections, with connections between the beam and each support such that it can be assumed that the support does not transfer significant bending moment to the beam. At the internal supports the beam may have either effective reinforcement or only nominal reinforcement. Beam-to-column connections in steelwork are classified in Eurocode 3: Part 1.1[11] both by stiffness, as:
nominally pinned,
rigid, or
semi-rigid
and by strength, as:
nominally pinned,
full-strength, or
partial-strengt
In Eurocode 4: Part 1.1, a composite connection is defined as: A connection between a composite member and any other member in which reinforcement is intended to contribute to the resistance of the connection. The system of classification is as for steel connections, except that semi-rigid connections are omitted, because design methods for them are not ye sufficiently developed. A full-strength and rigid connection has to be at least as stiff and strong as the beams connected, so a continuous composite beam can be analyzed for bending moments as one long member without internal connections, by methods to be explained in Section 4.3. Bridge girders (Volume 2) are usually of this type. The example to be used here is a two-span beam continuous over a wall or supporting beam. In multi-bay plane frames, commonly used in structures for buildings, the beam-to-column connections are often nominally pinned. The beams are then designed as simply-supported, where full-strength connections are used, the frame should be analysed as a whole, and the beams are not continuous as defined above. These beams are referred to here as beams in frames, as are those with partial-strength connections. In comparison with simple spans, beams in frames have the same advantages and disadvantages as continuous beams. The global analysis is more complex than for continuous beams, because the properties of columns and connections are involved, but the design of hogging moment regions of the beams is the same. In Section 4.3 on global analysis, only continuous beams are considered. For a given floor slab and design load per unit length of beam, the advantages of continuous beams over simple spans are:
higher span/depth ratios can be used, for given limits to deflections;
cracking of the top surface of a floor slab near internal columns can be controlled, so that the
use of brittle finishes (e.g. terrazzo) is feasible;
the floor structure has a higher fundamental frequency of vibration, and so is less susceptible
to vibration caused by movements of people;
the structure is more robust (e.g. in resisting the effects of or explosion).
The principal disadvantage is that design is more complex. Actions on one span cause action effects in adjacent spans, and the stiffness and bending resistance of a beam very along its length. It is not possible to predict accurately the stresses or deflections in a continuous beam for a given set of actions. Apart from the variation over time caused by the shrinkage and creep of concrete, there are the effects of cracking of concrete. In reinforced concrete beams, these occur at all cross-sections, and so have little influence on distributions of bending moment. In composite beams, significant tension in concrete occurs only in hogging regions. It is influenced by the sequence of construction of the slab, the method of propping used (if any), and by effects of temperature, shrinkage, and longitudinal slip.
The flexural rigidity of a fully cracked composite section can be as low as quarter of the uncracked value, so a wide variation in flexural rigidity can occur along a continuous beam of uniform section. This leads to uncertainty in the distribution of longitudinal moments, and hence in the amount of cracking to be expected. The response to a particular set of actions also depends on whether it precedes or follows another set of actions that causes cracking in a different part of the beam.
For these reasons, and also for economy, design is based as far as possible on predictions of ultimate strength (which can be checked by testing) rather than on analyses based on elastic theory. Methods have to be developed from simplified models of behaviour. The limits set to be scope of some models seem arbitrary, as they correspond to the range of available research data, rather than to known limitations of the model.
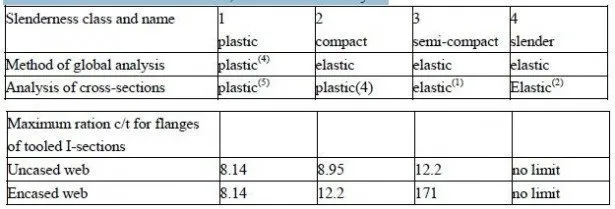
Almost the whole of Chapter 3, on simply-supported beams and slabs, applies equally to the sagging moment regions of continuous members. The follows of hogging moment regions of beams are treated in Section 4.2, which applies also to cantilevers. Then follows the global analysis of continuous beams, and the calculations of stresses and deflections. Both rolled steel I- or H-sections and small plate or box girders are considered, with or without web encasement and composite slabs. It is always assumed that the concrete slab is above the steel member, because the use of slabs below steel beams with which they are composite is almost unknown in buildings, though it occurs in bridges.