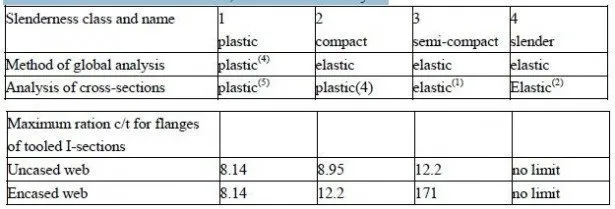
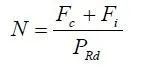Cross-sections in Class 1 or 2
The methods of calculation for sections in Class 1 or 2 are in principle the same as those for composite slabs, explained in Section 3.3.1, to which reference should be made. The main assumptions are as follows:
the tensile strength of concrete is neglected;
plane cross-sections of the structural steel and reinforced concrete parts of a composite section each remain plane;
and, for plastic analysis of sections only;
the effective are of the structural steel member is stressed to its design yield strength f y/γa in tension or compression;
the effective area of concrete in compression resists a stress of 0.85 fy /γa constant over the whole depth between the plastic neutral axis and the most compressed fibre of the concrete. In deriving the formulae below, it is assumed that the steel member is a rolled 1-section, of cross-sectional area Aa, and the slab is composite, with profiled sheeting that spans between adjacent steel members. The composite section is in Class 1 or 2, so that the whole of the design load can be assumed to be resisted by the composite member, whether the construction was propped or unpropped. This is because the inelastic behaviour that precedes flexural failure allows internal redistribution of stresses to occur.
The effective section is shown in Fig.3.15(a). As for composite slabs, there are three common situations, as follows. The first two occur only where full shear connection is provided.
(1) Neutral axis within the concrete slab The stress blocks are shown in Fig.3.15(b). the depth x, assumed to be the position of the plastic neutral axis, is found by resolving longitudinally:

Taking moments about the line of action of the force in the slab.

where g h defines the position of the centre of area of the steel section, which need not be symmetrical about its major (y-y) axis.
(2) Neutral axis within the steel top flange
The force Ncf, given by
(3) Partial shear connection
The symbol Nct was used in paragraphs (1) and (2) above for consistency with the treatment of composite slabs in Eurocode 4 and in Section 3.3.1. In design, its value us always the lesser o the two values given by equations (3.56) and (3.58). It is the force which the shear connectors between the section of maximum sagging moment and each free end of the beam (a shear span) must be designed to resist, if full shear connection is to be provided. In draft Eurocode 4; Part 1.1 the symbol used in the clause on partial shear connection in beams is Fcf, so in this explanation it is used in place of Ncf.
Let us suppose that the shear connection is designed to resist a force Fc, smaller than Fcf. If each connector has the same resistance to shear, and the number in each shear span is N, then the degree of shear connection is defined by:

Where Nf is the number of connectors required for full shear connection. The plastic moment of resistance of a composite slab with partial shear connection had to be derived in Section 3.3.1(3) by an empirical method, because the flexural properties of profiled sheeting are to complex. For composite beams, simple plastic theory can be used.
The depth of the compressive stress block in the slab, xc, is given by

and is always less than hc. The distribution of longitudinal strain in the cross-section is intermediate between the two distributions shown (for stress) in Fig.2.2(c), and is shown in Fig.3.15(d), in which C means compressive strain. The neutral axis in the slab is at a depth xn greater than xc, as shown.
In design of reinforced concrete beams and slabs it is generally assumed that xa / xc is between 0.8 and 0.9. The less accurate assumption xa = xc is made for composite beams and slabs to avoid the complexity that otherwise occurs in design when xa = hc or, for beams with non-composite slabs, a c x ≈ h . This introduces as error in pl M that is on the unsafe side, but is negligible for composite beams. It is not negligible for composite columns, where it I allowed for (Section 5.6.5.1).
There is a second neutral axis within the steel 1-section. If it lies within the steel top flange, the stress block are as shown in Fig.3.15(c), except that the block for the force Nct is replaced by a shallower one, for force Fe. By analogy with equation (3.62) the resistance moment is

The curve is not valid for very low degrees of shear connection, for reasons explained in Section 3.6.2. Where it is valid, it is evident that a substantial saving in the cost of shear connectors can be slightly below pl Rd M . .
Where profiled sheeting is used, there is sometimes too little space in the troughs for Nt connectors to be provided within a shear span, and then partial-connection design becomes essential.
Unfortunately, curve ABC in Fig.3.16 cannot be represented by a simple algebraic expression. In practice, it is therefore sometimes replaced (conservatively) by the line AC, given by
where PRd is the design resistance of one connector.
The design of shear connection I considered in greater depth in Section 3.6.
Variation in bending resistance along a span In design, the bending resistance of a simply-supported beam is checked first at the section of maximum sagging moment, which is usually at midspan. For a steel beam of uniform section, the
bending resistance is then obviously sufficient, elsewhere within the span; but this may not be so for a composite beam. Its bending resistance depends on the number of shear connectors between the nearer end support and the cross-section considered. This is shown by curve ABC IN Fig.3.16, because the x coordinate is proportional to the number of connectors.
Suppose, for example, that a beam of span L is deigned with partial shear connection and N / Nt== 0,5 idspan. Curve ABC is redrawn in Fig.3.17(a), with the bending resistance at midspan, MPl Rd . , denote by B. If the connectors are uniformly spaced along the span, as is usual
in buildings, then the axis N/Nf is also an axis x/L, where x is the distance from the nearer support,
and N is the number of connectors effective in transferring the compression to the concrete slab
over a length x from a free end. Only these connectors can contribute to the bending resistance
pl Rd M . , at that section, denoted E in Fig.3.17(b). In other words, bending failure at section E
would be caused (in the design mode) by longitudinal shear failure along length DE of the
interface between the steel flange and the concrete slab…