A truss is an assemblage of straight members connected at their ends by flexible connections to form a rigid configuration. Because of their light weight and high strength, trusses are widely used, and their applications range from supporting bridges and roofs of buildings (Fig. 4.1) to being support structures in space stations (Fig. 4.2). Modern trusses are constructed by connecting members, which usually consist of structural steel or aluminum shapes or wood struts, to gusset plates by bolted or welded connections.
As discussed in Section 1.4, if all the members of a truss and the applied loads lie in a single plane, the truss is called a plane truss.
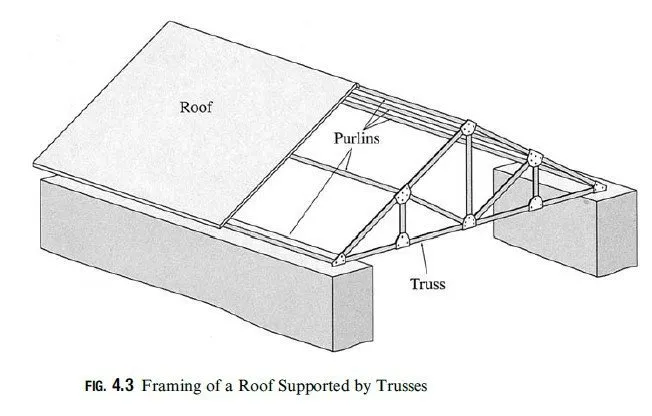
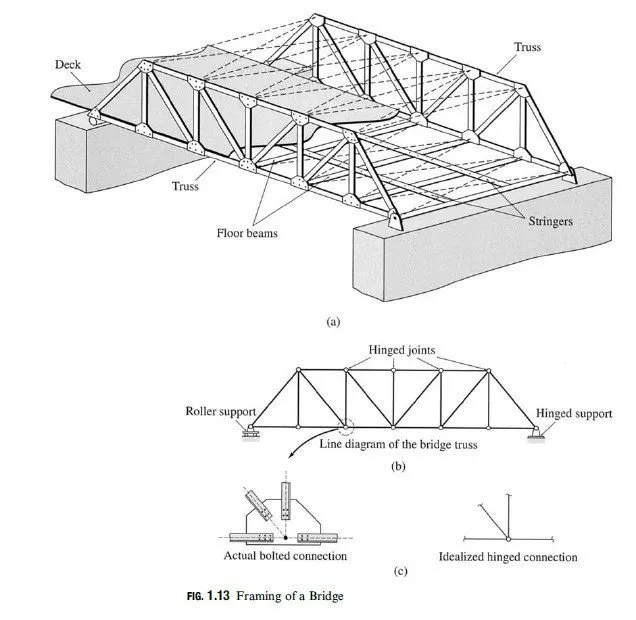
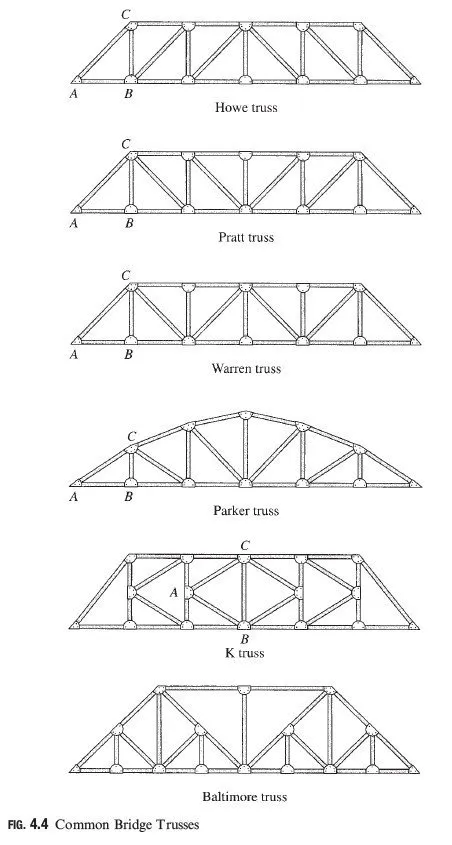
Plane trusses are commonly used for supporting decks of bridges and roofs of buildings. A typical framing system for truss bridges was described in Section 1.4 (see Fig. 1.13(a)). Figure 4.3 shows a typical framing system for a roof supported by plane trusses. In this case, two or more trusses are connected at their joints by beams, termed purlins, to form a three-dimensional framework. The roof is attached to the purlins, which transmit the roof load (weight of the roof plus any other load due to snow, wind, etc.) as well as their own weight to the supporting trusses at the joints. Because this applied loading acts on each truss in its own plane, the trusses can be treated as plane trusses. Some of the common configurations of bridge and roof trusses, many of which have been named after their original designers, are shown in Figs. 4.4 and 4.5 (see pp. 92 and 93), respectively.
Although a great majority of trusses can be analyzed as plane trusses, there are some truss systems, such as transmission towers and latticed domes (Fig. 4.6), that cannot be treated as plane trusses because of their shape, arrangement of members, or applied loading. Such trusses, which are called space trusses, are analyzed as three-dimensional bodies subjected to three-dimensional force systems.
The objective of this chapter is to develop the analysis of member forces of statically determinate plane and space trusses. We begin by discussing the basic assumptions underlying the analysis presented in this chapter, and then we consider the number and arrangement of members needed to form internally stable or rigid plane trusses. As part of this discussion, we define simple and compound trusses. We also present the equations of condition commonly encountered in plane trusses. We next establish the classification of plane trusses as statically determinate, indeterminate, and unstable and present the procedures for the analysis of simple plane trusses by the methods of joints and sections. We conclude with an analysis of compound plane trusses, a brief discussion of complex trusses, and analysis of space trusses.
4.1 Assumptions for Analysis of Trusses
4.2 Arrangement of Members of Plane Trusses-Internal Stability
4.3 Equations of Condition for Plane Trusses
4.4 Static Determinacy, Indeterminacy, and Instability of Plane Trusses
4.5 Analysis of Plane Trusses by the Method of Joints
4.5.1 Plane Trusses by the Method of Joints Problems and solutions
4.6 Analysis of Plane Trusses by the Method of Sections
4.6.1 Plane Trusses by the Method of Sections Problems and Solutions
4.7 Analysis of Compound Trusses
4.7.1 Compound Trusses Problems ans Solutions
4.8 Complex Trusses
4.9 Space Trusses