Now consider the same bearing wall of the previous example, but make the gravity load eccentric. As before, suppose that the load is applied over a 4-in. bearing plate, and assume that bearing stresses vary linearly under the bearing plate as shown in Fig. 5.13. Then the eccentricity of the applied load with respect to the centerline of the wall is
At each horizontal plane through the wall, the following conditions must be met:
Maximum compressive stress from factored axial loads must not exceed the slenderness-dependent values in Eqs. (3-12) or (3-13) as appropriate, reduced by a φ-factor of 0.60.
Maximum compressive stress from factored loads (including a moment magnifiers) must not exceed 0.80 f ² m in the extreme compression fiber, reduced by a φ-factor of 0.60.
Maximum tension stress from factored loads (including a moment magnifier) must not exceed the modulus of rupture in the extreme tension fiber, reduced by the φ-factor of 0.60.
For each condition, the more critical of the two possible loading combinations must be checked. Because there is no wind load, this example will be worked using that the loading combination 1.2D + 1.6L.
We must check various points on the wall. Critical points are just below the roof reaction (moment is high and axial load is low, so maximum tension may govern); and at the base of the wall (axial load is high, so maximum compression may govern). Check each of these locations on the wall. As before, try 8-in. nominal units, and a specified compressive strength, f ² m, of 1500 lb/in.2. This can be satisfied using units with a netarea compressive strength of 1900 lb/in.2, and Type S PCL mortar. Work with a strip with a width of 1 ft (measured along the length of the wall in plan). Stresses are calculated using the critical section, consisting of the bedded area only (2008 MSJC, Sec. 1.9.1.1). Just below the roof reaction, the axial force is
Pu= 1.2 (700 lb) + 1.6 (350 lb) + 1.2 (3.33 ft × 48 lb/ft) = 1592 lb
To calculate stiffness-related parameters for the wall, we use the average cross section, corresponding to the fully bedded section in the table (2008 MSJC Code, Sec. 1.9.3).

Because the factored axial force is much less than slenderness-dependent nominal capacity, reduced by the appropriate φ factor, the axial force check is satisfied.
Now check the net compressive stress. Because the loading is eccentric, there is bending stress:
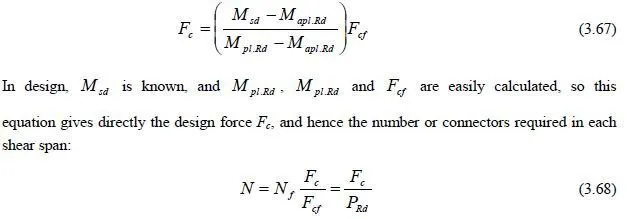
The net compressive stress does not exceed the prescribed value. Clearly, because this example involves eccentric axial loads, the first criterion (axial load reduced by slenderness effects) is less severe than the second (maximum compressive stress from axial loads and bending moments).
Because the bending stress from factored design moments (42.9 lb/in.2) is less than the axial stress from factored axial load (53.1 lb/in.2), there is no net tension, and the third criterion (net tension) is automatically satisfied.
Section 3.2.2.4 of the 2008 MSJC Code requires that magnified moments be checked. For this wall, the ratio of (h/r) is 70.5, which exceeds 45. Therefore a magnifier must be calculated.
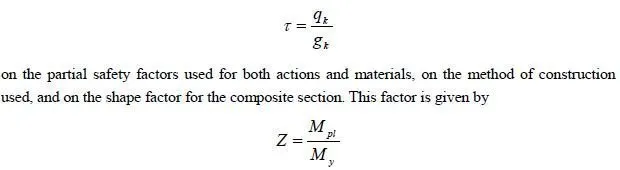
This is very close to 1.0 and does not affect the previous checks.
The other critical section could be at the base of the wall, where the checks of all three criteria are identical to those of example in Sec. 5.2.3, plus the moment magnifier. All are satisfied, and the design is therefore satisfactory.
