Construct the moment-axial force interaction diagram by the strength approach for a nominal 8-in. CMU wall, fully grouted, with fm² = 1500 lb/in.2 and reinforcement consisting of #5 bars at 48 in., placed in the center of the wall. Compute the interaction diagram per foot of wall length. For the case of a wall with reinforcement at mid-depth, the reference axis for moment is located at the plastic centroid (geometric centroid) of the cross-section, which is also at mid-depth. This leads to results which appear considerably different from what we are used to for a symmetrically reinforced column. For example, using the geometric centroid (the level of the reinforcement) as the reference axis, the contribution of the reinforcement to the moment is always zero. In what is apparently even stranger, the balanced-point axial force does not coincide with the maximum moment capacity. As a result, hand calculations are useful for some reinforced masonry beam-columns, but not all.
Pure Compression
Because the compressive reinforcement in the wall is not supported laterally, it is not counted in computed the capacity.



Plot of Strength Interaction Diagram by Hand
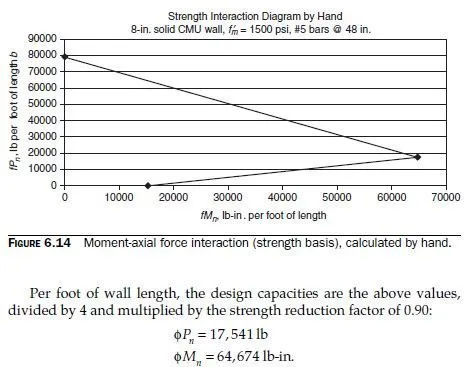
The strength-basis moment-axial force interaction diagram calculated above is plotted in Fig. 6.14.
As we shall shortly see, the points that we have calculated are correct. The form of the diagram is misleading, however, because the balance point is actually not the point of maximum moment. It is incorrect to draw the diagram with a straight line from the balance point to the purecompression point. The balance point becomes the point of maximum moment as the reinforcement is placed farther apart than about 70 percent of the thickness of the wall.