PASSIVE STATE In Fig. 11.18, the notations used are the same as in Fig. 11.17. As the wall moves into the backfill, the soil tries to move up on the pressure surface AB which is resisted by friction of the surface. Shearing stress on this surface therefore acts downward. The passive earth pressure P is the resultant of the normal pressure P and the shearing stress. The shearing force is rotated upward with an angle 8 which is again the angle of wall friction. In this case S is positive. As the rupture takes place along assumed plane surface AC, the soil tries to move up the plane which is resisted by the frictional force acting on that line. The shearing stress therefore, acts downward. The reaction R makes an angle 0 with the normal and is rotated upwards as shown in the figure. The polygon of forces is shown in (b) of the Fig. 11.18. Proceeding in the same way as for active earth pressure, we may write the following equations:
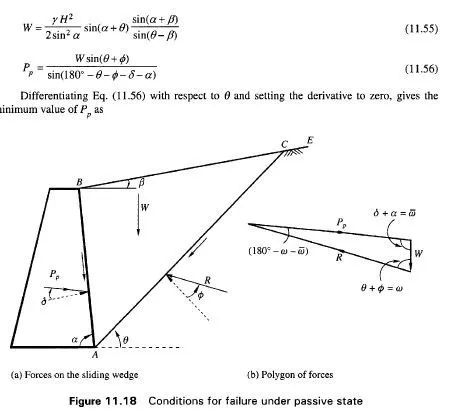
Coulomb sliding wedge theory of plane surfaces of failure is valid with respect to passive pressure, i.e., to the resistance of non-cohesive soils only. If wall friction is zero for a vertical wall and horizontal backfill, the value of Kp may be calculated using Eq. (11.59). If wall friction is considered in conjunction with plane surfaces of failure, much too high, .and therefore unsafe values of earth resistance will be obtained, especially in the case of high friction angles 0. For example for 0= 8 = 40°, and for plane surfaces of failure, Kp = 92.3, whereas for curved surfaces of failure Kp = 17.5. However, if S is smaller than 0/2, the difference between the real surface of sliding and Coulomb’s plane surface is very small and we can compute the corresponding passive earth pressure coefficient by means of Eq. (11.57). If S is greater than 0/2, the values of Kp should be obtained by analyzing curved surfaces of failure.

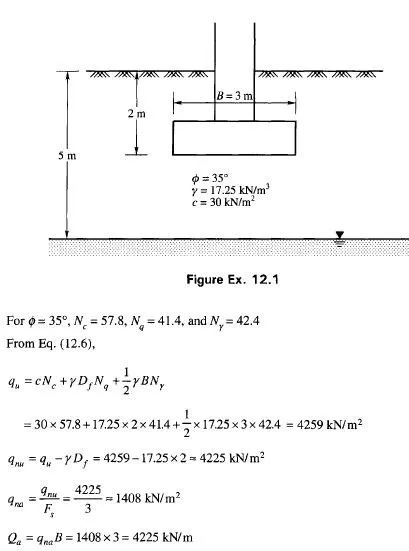

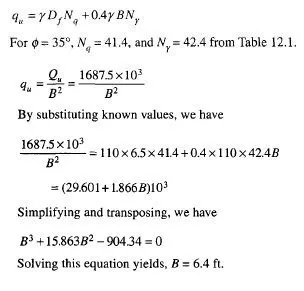
Greetings,
I cant seem to see anything for Coulomb’s earth pressure theory for sand for active state. is the link down or content removed? Doing some comparison between the Coulomb Close Form solution and a Force Polygon method for both passive and active conditions but the error seems large. Have got a difference of 18% between both methods. Your notes are very helpful. Hope the link of active state can be revived.
Regards,
weishung