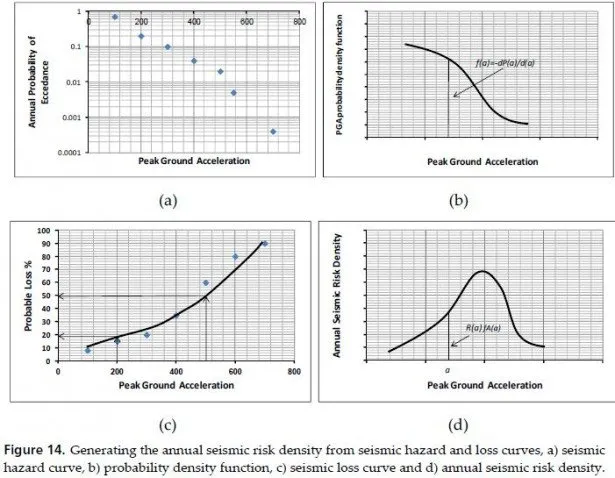
Soil in reality is considerably non-linear. That is why H.B.Seed [23] suggested special method to describe seismic response of horizontally-layered soil to the verticallypropagating free-field seismic waves by equivalent linear model. Parameters of this model are obtained in iterative calculations, as modules and damping in each layer are straindependent.
This method is used in the famous SHAKE code [24]. Usually 7-8 iterations are enough to get the error less than 1%.
SHAKE calculations may be started from the surface (i.e. surface motion is given; for each other layer the motion is to be calculated together with equivalent soil properties); this case is called deconvolution. On the contrary, SHAKE calculations may be started from some depth where the motion is given; this case is called convolution. Motion for one and the same point in depth may be given in one of two variants. The first variant is just a motion of the point inside soil composed of the upcoming wave and wave coming down (see the 1D example in p.5 above). The second variant is to set just the upcoming wave amplitude. Sometimes this motion is called outcropped motion, because they double the upcoming wave amplitude, like it is at the free surface (see the example in p. 6.1 above). However, such a doubled motion will be similar to the motion of the really outcropped surface only at the surface of the underlying homogeneous half-space, and not in the middle of the layered soil.
The typical case consists of two sequential SHAKE calculations. First, deconvolution is performed using the initial soil model and initial seismic motion of the free surface of the initial soil (the author usually calls it foundation no.1). Note, that the underlying halfspace is not modified in the process of SHAKE iterations. That is why one should include into the modified part at least one upper layer of half-space. After the deconvolution is through, one should change the half-space manually making parameters equal to the lowest modified layer. The main result of deconvolution is an outcropped motion of the halfspace surface. The second stage is a convolution. Half-space stays the same as in deconvolution (after manual modification), but the upper layers may change due to various reasons starting from the direct changes in the construction process (very often the upper several meters of the initial soil are withdrawn). Sometimes the weight of the future structure changes the properties of the soil. Anyhow, we generally have foundation no.2 instead of the first soil foundation. In the convolution procedure the outcropped motion of the half-space surface is given, and the whole wave field with equivalent soil properties is obtained as a result together with motion of the new surface.
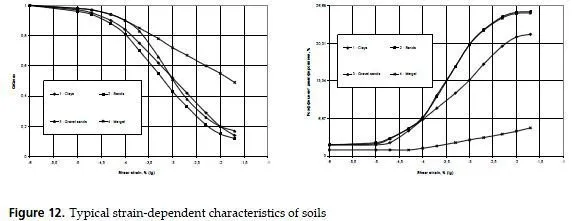
Typical strain-dependent characteristics of different soils are shown on Fig.12. Sometimes they call it degradation curves.
One should remember that degradation curves for shear modulus G are given in relative terms G/G0, where G0 is a low-strains value. On the contrary, strain-dependent characteristics of the internal damping are given for dimensionless coefficients without using low-strain values.
Typical results of SHAKE calculations for three levels of seismic intensity are given on Fig.13. Abbreviations of the level names mean: OBE operational basis earthquake; SSE safe shutdown earthquake (operations and shutdown refer to nuclear reactors activity). The results are calculated separately in two vertical planes (OXZ and OYZ) and then averaged (usually in two planes they are close to each other for every layer).
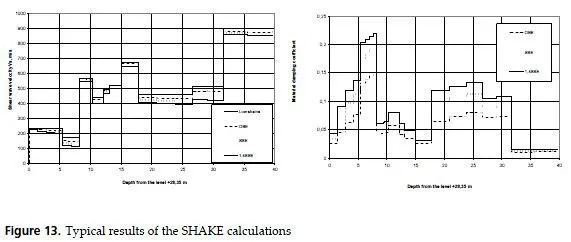
We see that near the surface the equivalent soil characteristics are close to the low-strain values. This is because of zero strains at the free surface for every intensity level.
Usually the greatest relative shift in velocities and damping is at the bottom of soft soil layers. If the intensity is very high, the iterations during deconvolution may not converge.
Physically it means that the given surface motion is no longer compatible with given soil properties; such motion cannot be transferred by given soil to the surface.
Both SHAKE results profiles of wave velocities/damping and surface motion are further on used in SSI analysis.
Theoretically a wide range of nonlinearities can be described by strain-dependent properties. However, these properties should be transient, i.e. they should vary from one time point to another during one seismic event. In the Seeds approach these properties in each soil layer are established once for the whole event duration (changing not from time to time, but from one linear run to another one). So, in fact soil properties depend not on the instant transient strains, but on some effective strains (in practice – on some portion of the maximal strain over the duration). In fact, Seed provided a tool to extrapolate the results of the lab test with harmonic excitation of the soil sample to another situation with nonharmonic wave in the same sample.
Nowadays seismologists are ready to provide more sophisticated approaches to the soil description. They can model accelerations in the soil more accurately with truly transient soil properties. But in the SSI problems (e.g., in SASSI or CLASSI) one will need linear soil with effective soil properties, so SHAKE still remains the best pre-SSI processor.
The result of SHAKE is obtained for horizontally-layered soil without structure. So, they say, that it contains primary non-linearity. The same equivalent strain-dependent properties can be further applied in the SSI problems to account for the secondary nonlinearity caused by structure, but the result will spoil horizontally-layered geometry of the soil. As we know, that will spoil CLASSI model and create additional problems in SASSI model.
That is why modern standards (e.g., ASCE4-98) require the consideration of the primary non-linearity, but do not require consideration of the secondary non-linearity of the soil.
Looking at soil-structure system, one can find nonlinearities not only in soil, but at the contact surface. Even if both soil and structure are modeled by linear systems, they may have various contact terms. Most often full contact is assumed it does not spoil linearity.
However, soil tension (unlike soil compression) is very limited, and that may cause a) uplift of the base mat from the soil, b) separation of the embedded basement walls from the soil.
Base mat uplift may be estimated if linear full contact vertical forces over contact surface Q are compared to the static vertical forces caused by structural weight. In practice the full uplift is seldom met, but rocking of the structure can cause dynamic tension near the edges of the base mat. This partial dynamic uplift usually occurs for stiff soils and sizable structures. Does it change the response motion considerably? Today they believe that if the area of partial dynamic uplift is less than 1/3 of the total contact area, one can neglect this uplift and still use SSI linear model with full contact.
Separation of vertical embedded walls is treated as follows. In the upper half of the embedment depth (but only up to 6 meters from the surface) they break soil-structure contact completely. Below this level they assume full contact.