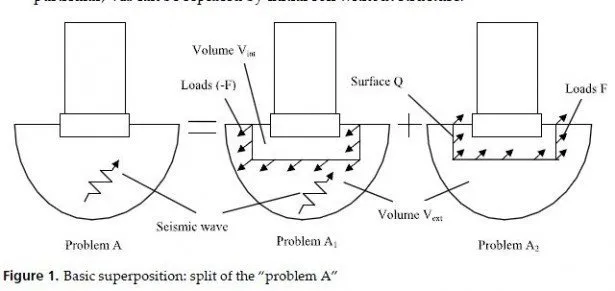
As to the topographic surface, the discrete grid must conform to the free surface to suppress artificial scattered waves. Such grid is named boundary-conforming grid (Hvid, 1994;
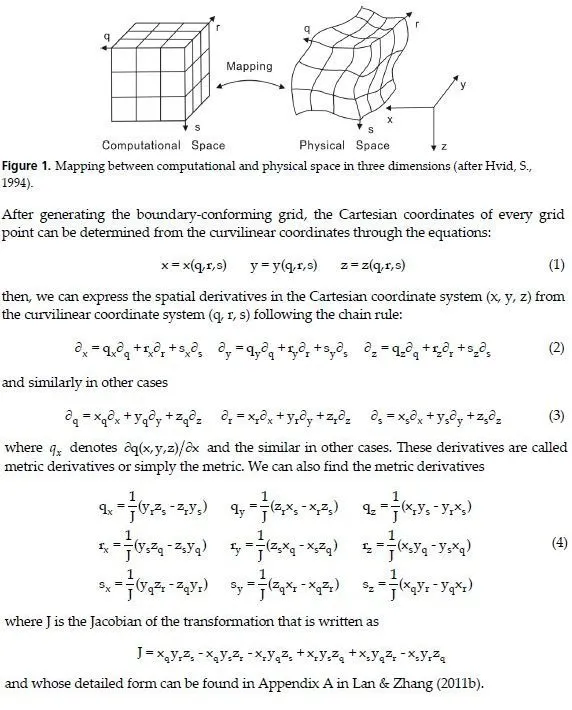
Thompson et al., 1985), and it was early used by Fornberg (1988) in seismic wave simulation with the pseudo-spectral method. A grid of this type is achieved by carrying out a transformation between the (curvilinear) computational space and the (Cartesian) physical space as illustrated in Figure 1. By means of this transformation, the curvilinear coordinates q, r and s are mapped into Cartesian coordinates within the physical space, where both systems have positive direction downward for the vertical coordinate. A boundary in the physical space presents a constant value of one of the curvilinear coordinates-be it a curve in two dimensions or a surface in three dimensions.
Boundary conforming grids may be of two fundamentally different types: structured and unstructured (or irregular) grids. A structured type grid (Figure 1) is characterized by having a fixed number of elements along each of the coordinate directions. The general element is a hexahedron in 3D, just as in the left panel of Figure 1. Neighboring elements in the physical space are also adjacent in the computational space, which is one of the great advantages of this type of grid. This property makes it relatively simple to implement in a computer. Structured grids are mainly used in finite difference and finite volume solvers.
Here, we focus on structured boundary conforming grids. Several methods may be used to generate these grids, namely: Partial Differential Equation (PDE) methods, algebraic methods, co-normal mapping methods and variational methods. Here we use PDE methods (see Hvid, 1994; and Thompson et al., 1985 for details).
It is worthful to note that even if the mapping equations (1) are given by an analytic function, the derivatives should still be calculated numerically to avoid spurious source terms due to the coefficients of the derivatives when the conservation form of the momentum equations are used (Thompson et al., 1985). In all examples presented in this paper the metric derivatives are computed numerically using second-order accurate finite difference approximations.