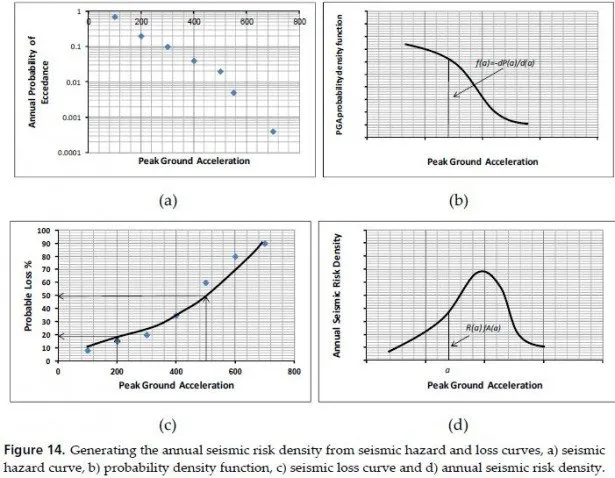
In Southern California, preliminary 3D earth structure models are already available, and efficient numerical methods have been developed for 3D anelastic wave-propagation simulations. We develop an algorithm to utilize these capabilities for rapid full-wave centroid moment tensor (CMT) inversions. The procedure relies on the use of receiver Green tensors (RGTs), the spatial-temporal displacements produced by the three orthogonal unit impulsive point forces acting at the receivers. Once we have source parameters of earthquakes, a nearreal time full-wave ground motion map, that considers both source and wave-propagation effects in a 3D structure model, may also available for earthquake early warning purposes.
In our CMT inversion algorithm, the RGTs are computed in our updated 3D seismic structure model for Southern California using the full-wave method that allows us to account for 3D path effects in our source inversion. The efficiency of forward synthetic calculations could be improved by storing RGTs and using reciprocity between stations and any spatial grid point in our model. In our current model, we will use three component broadband waveforms below 0.2 Hz to invert source parameters. Based on Kikuchi and Kanamoris [23]source inversion method, any moment tensor can be expressed as linear combination of 6 elementary moment tensors. In our current coordinate (x=east, y=north,
z=up), the moment tensor can be expressed as below:

There are two main advantages of using this method. First, different subsets of 6 elementary
moment tensors could represent different source parameter assumptions such as M1~M6
could recover general moment tensors and M1~M5 could represent pure-deviatoric moment
tensors [23]. From efficiency point of view, we only need to generate synthetic waveforms of
6 elementary moment tensors at grid points close to initial sources locations for receivers to
invert an optimal CMT solution.
For centroid location x1 and centroid time t1, the synthetic seismograms of 6 elementary
moment tensors could be defined as:

From inversion point of view, the phases have less structure heterogeneous effects can reduce the nonlinear effects caused by complex 3D structure such as body wave phases that propagate through relative simple deep structure and surface wave phases that propagate along free surface and average out the heterogeneity. We apply our seismic waveform segmentation algorithm that is based on continuous wavelet transforms and a topological watershed method to observed seismograms and then select the first (potential body wave) and biggest (potential surface wave) time-localized waveforms to invert source parameters.
In source inversion, we applied a multi-scale grid-searching algorithm based on Bayesian inference to find an optimal solution [Figure 4]. We consider a random vector H composed of 6 source parameters: the longitude, latitude and depth of the centroid location rS, and the strike, dip and rake of the focal mechanism. We assume a uniform prior probability P0(H) over a sample space Ω0, which is defined as a sub-grid in our modeling volume centered around the initial hypocenter location provided by the seismic network with grid spacing in three orthogonal directions given by a vector θ0 and a focal mechanism space with the ranges given by 0°â‰¤ strike ≤360°, 0°â‰¤ dip ≤90° and -90°â‰¤ rake ≤90° and with angular intervals in strike, dip and rake specified by a vector ï±0.
We apply Bayesian inference in three steps sequentially. In the first step, the likelihood function is defined in terms of waveform similarity between synthetic and observed seismograms. We quantify waveform similarity using a normalized correlation coefficient (NCC) defined as


A very low P0(NCCn) indicates that the nth observed waveform cannot be fit well by any solutions in our sample space. This may be due to instrumentation problems or unusually high noise levels in the observed waveform data.
In the second step, we apply the same algorithm on another measurements, time-shifts between the observed and synthetic waveforms when the NCC is the maximum in allowed time-shift range. The last step is applying the same processes to the amplitude ratio measurements. By using the Bayesian approach, we can obtain the probability density functions of source parameters that contain uncertainties information rather than a single best solution. Our optimal source parameter solution is the one with highest probability. In Figure 4, examples of the marginal probabilities for some of the source parameters are shown for the 3 September 2002 Yorba Linda earthquake.
For earthquake early warning purposes, there are few approaches to make our CMT inversion method toward (near) real time and then use optimal CMTs for generating full-wave peak ground motion maps. To save some time in generating synthetic seismograms, we can store synthetic seismograms of 6 elementary moment tensors rather than extract them from RGTs.
Destructive or larger earthquakes tend to occur in existing fault zones or regions where earthquakes occurred. Based on the assumption above, rather than store synthetic seismograms of all grid points in our model, we can store the synthetic seismograms of grid points near fault zones or high seismicity regions. Another possibility is to save time of inversion by using other efficient inversion algorithms. Full-wave ground motion prediction maps could be generated based on the synthetic seismograms of optimal CMT solutions.

The speed of earthquake source parameters estimation and accurate ground motion predictions are both play essential role in earthquake early warning systems. In the ElarmS, earthquake locations, origin time and magnitudes could be inverted in very short time. Peak ground motion maps can be generated shortly by using empirical attenuation relations. The CMT inversion method we proposed has potential for (near) real time inversion and then solutions could be used for (near) real time full-wave peak ground motion maps. In addition, the Bayesian approach used in our CMT inversion has uncertainty of solutions and could be projected into ground motion estimations.