The reliability of a structural system or lifeline may be referred to as the ability of the system or its components to perform their required functions under stated conditions for a specified period of time. Because of uncertainties in loading and capacity, the subject usually includes probabilistic methods and is often made through indices such as a safety index or the probability of the failure of the structure or lifeline.
2.1.1. Reliability index and failure
To evaluate the seismic performance of the structures, performance functions are defined.
Let us assume that z=g(x1, x2, ¦,xn) is taken as a performance function. As such, failure or damage occurs when z
Pf=P[z
Simply assume that z=EDP-C where EDP stands for Engineering Demand Parameter and C is the seismic capacity of the structure.
Damage or failure in a structural system or lifeline occurs when the Engineering Demand Parameter exceeds the capacity provided. For example, in a bridge structural damage may refer to the unseating of the deck, the development of a plastic hinge at the bottom of piers or damage due to the pounding of the decks to the abutments, etc.
Given that EDP and C are random parameters having the expected or mean values of μEDP and μC and standard deviation of σEDP and σC, the safety index or reliability index, β, is defined as:
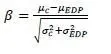
It has been observed that the random variables such as “EDP” or “C” follow normal or lognormal
distribution. Accordingly, the performance function, z, also will follow the same
distribution. Accordingly, probability of failure (or damage occurrence) may be expressed as
a function of safety index, as follows:

Engineering demand parameters
The Engineering Demand Parameters describe the response of the structural framing and the non-structural components and contents resulting from earthquake shaking. The parameters are calculated by structural response simulations using the IMs and corresponding earthquake motions. The ground motions should capture the important characteristics of earthquake ground motion which affect the response of the structural framing and nonstructural components and building contents. During the loss and risk estimation studies, the EDP with a greater correlation with damage and loss variables must be employed.
The EDPs were categorized in the ATC 58 task report as either direct or processed [9]. Direct EDPs are those calculated directly by analysis or simulation and contribute to the risk assessment through the calculation of P[EDP | IM]; examples of direct EDPs include interstory drift and beam plastic rotation. Processed EDPs – for example, a damage index – are derived from the values of direct EDPs and data on component or system capacities.
Processed EDPs could be considered as either EDPs or as Damage Measures (DMs) and, as such, could contribute to risk assessment through P[DM | EDP]. Direct EDPs are usually introduced in codes and design regulations. For example, the 2000 NEHRP Recommended Provisions for Seismic Regulations for Buildings and Other Structures introduces the EDPs presented in Table 2 for the seismic design of reinforced concrete moment frames [12-13]:

Processed EDPs are efficient parameters which could serve as a damage index during loss and risk estimation for structural systems and facilities. A Damage Index (DI), as a singlevalued damage characteristic, can be considered to be a processed EDP [10]. Traditionally, DIs have been used to express performance in terms of a value between 0 (no damage) and 1 (collapse or an ultimate state). An extension of this approach is the damage spectrum, which takes on values between 0 (no damage) and 1 (collapse) as a function of a period. A detailed summary of the available DIs is available in [14].
Park and Angin [15] developed one of the most widely-known damage indices. The index is a linear combination of structural displacement and hysteretic energy, as shown in the equation:
See Powell and Allahabadi, Fajfar, Mehanny and Deierlein, as well as Bozorgnia and Bertero for more information about other DIs in [16-19].