Calculational method of SMZ is used in order to analyse features of soil behavior with introduction of definite engineeringgeological structure characteristics of investigated site as initial data: values of transverse wave velocities, index of extinction, modulus of elasticity, power of soil layers, their consistency etc. Calculational method includes thinlayer medium, multiple-reflected waves, finite-difference method, finite-elements analysis (FEA) and other techniques.
One can take nonlinear soil properties into account in the problems of earthquake engineering by means of instrumental and calculation methods. The instrumental method of SMZ is the main method. Nevertheless it is quite often necessary to solve such problems using calculational method, which allows to model practically any conditions, which are observed in the nature. At the same time the practice reqirements lead to the necessity of calculation of soil vibrations for the conditions of their nonlinear-elastic and nonelastic deformations. At the solution of such problem it is assumed that elastic half-space behaves as linear-elastic medium and the covering soil displays strong nonlinear properties at intensive seismic or dynamic influences (Bonnet & Heitz, 1994).
Instrumental stress-sstrain dependences can be used, for example one obtained for plastic clay soil shown in fig. 12. The conception of the so-called soil bimodularity, offered by A.V.Nikolaev (Nikolaev, 1987, Zaalishvili, 1996; 2000) is taken into account in the given dependence. Considerable differences in behavior of weak soils at compression and dilatation lie in the base of the phenomenon. Such soil is characterized at dilatation by quite small shear modulus.

Equivalent linear model. SHAKE and EERA programs
Equivalent linear model is one of the first models, which take nonlinear soil behavior into account. Equivalent linear approximation consists in modification of the model of Kelvin Voight (for taking some types of nonlinearity into account) and, for example, is realized in the programs SHAKE (Schnabel et al., 1972) and EERA (Bardet et al., 2000).
Equivalent linear model is based on the hypothesis that shear modulus G and attenuation coefficient ξ are the functions of shearing strain γ (fig. 18.1). In the programs SHAKE and EERA (Equivalent-linear Earthquake site Response Analyses) the values of shear modulus G and attenuation coefficient ξ are determined (in the process of iteration) so that they correspond to the deformation levels in each layer.
IM model. NERA program
In 2001 realization principle, which was used in the program EERA, was applied in the programming of NERA (Nonlinear Site Response Analysis) (Bardet, Tobita, 2001), which allows to compute soil thickness nonlinear reaction on seismic influences. The program is based on the medium model, offered by Iwan (1967) and Mroz (1967), which is often called the IM model for short. As it is shown in the fig. 18.2, the model supposes the simulating of nonlinear curves strain-deformation, using a number of n mechanical elements, which have different stiffness kj and sliding resistance Rj, where R1 < R2 < ¦ < Rn. Initially the residual stresses in all elements are equal to zero. At monotonically increasing load the element j deforms until the transverse strain Ï„ reaches Rj. After that the element j keeps positive residual stress, which is equal to Rj.
The equation, describes dynamics of soil medium, is solved by the method of central differences.
Calculation of nonlinear absorptive ground medium vibrations using multiple
reflected waves tool of seismic microzonation
Lets suppose that we have the seismic wave, which falls on the soil thickness surface. Lets assume that soil thickness is nonlinear absorptive unbounded medium with the density ï² and S-wave propagation velocity vS. At small deformations the value of shear modulus G will be maximum for the given soils:
![]()
At the deformation increase the value G remains constant at first but at reaching some value (which is definite for each material or soil) the value G considerably changes, i.e. the soil begins to display its nonlinear properties. At the continued deformation increase the growth of stresses decelerates and then can remain unchanged until material destruction or hardening, i.e. until structural condition change.
As the main soil index, which characterizes its type and behavior at intensive loads, the value of plasticity PI was chosen. The parameters, which are necessary for calculations, are determined on basis of empirical ratios (Ishibashi, Zhang, 1993):

where G is the current shear modulus, stress is normal stress. Seismic energy absorption is calculated by the formula

On basis of the given ratios and introduced by us ratios for determination of necessary indices (normal stress, deformation etc), nonlinear version of the program ZOND was worked out. From the database of strong motions AGESAS, which was formed by us (Zaalishvili et al., 2000), the accelerogram, which was recorded on rocks in Japan, with the characteristics (magnitude, epicentral distance, spectral features etc.) similar to the territory of Tbilisi city, was chosen as the accelerogram, given into the bedrock.
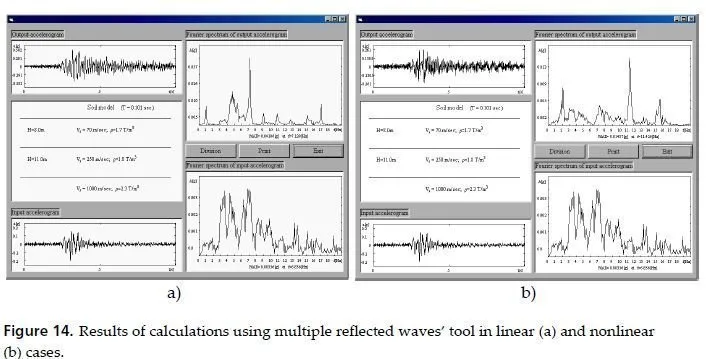
The analysis of the results of linear and nonlinear calculations models of definite areas of Tbilisi city territory confirms the adequacy of calculations to the physical phenomena, which were obtained in soils at intensive loads (fig. 13) (Zaalishvili, 2009). With the increase of seismic influence intensity the nonlinearity display increases. Absorption grows simultaneously. Hence the resulting motion at quite high influence levels can be lower than the initial level. It corresponds to the fact, which is known on the results of analysis of strong earthquake consequences, which happened in recent yares (for example, Northridge earthquake, 1994).
Calculation of nonlinear soil response using FEM tool of seismic microzonation The problem of the determination of soil massif response on dynamic influence with taking soil nonlinear properties into account can be solved by usage of finite element method (FEM) in the following way (Zaalishvili, 2009).
Soil medium is represented in the form of two-dimensional massif, which is approximate by triangular finite elements. The net, which consists of triangular elements, allows to describe quite accurately any relief form and form of the layer structure of soil massif with its physics-mechanical parameters. Within finite elemet the soil is homogeneous with inherent to it characteristics, which vary in time depending on influence intensity. Earthquake accelerogram of horizontal or vertical direction, which is applied, as a rule, to the foundation of soil massif, is used as the influence. Soil is in the conditions of plane deformation and is considered as an orthotropic medium. Axes of the orthotropy coincide with the directions of main strains.
The problem of nonlinear dynamics of soil massif is solved by means of the consecutive determination of mode of deflection of the system on the previous step. The system is linearelastic
on each step.