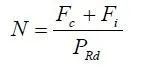It is now assumed that the two halves of the beam shown in Fig.2.2 are joined together by an infinitcly stiff shear connection. The two members then behave as one. Slip and slip strain are everywhere zero, and it can be assumed that plane sections remain plane. This situation is known as full interaction. With one exception (Section 3.5.3), all design of composite beams and columns in practice is based on the assumption that full inter-action is achieved.
For the composite beam of breadth b and depth 2h ,I=2bh3/3,and elementary theory gives the midspan bending moment as wL2/8,The extreme fibre bending stress is
which is one-quarter of the previous deflection (equation(2.3)),Thus the provision of shear connection increases both the strength and the stiffness of a beam of given size, and in practice leads to a reduction in the size of the beam required for a given loading, and usually to a reduction in its cost.
In this example-but not always-the interface AOB coincides with the neutral axis of the composite member, so that the maximum longitudinal shear stress at the interface is equal to the maximum vertical shear stress, which occurs at x = ±L / 2 and is 3WL/8bh, from (2.10).
The shear connection must be designed for the longitudinal shear per unit length, v, which is known as the shear flow, In this example it is given by

The total shear flow in a half span is found, by integration of equation (2.12), to be 3wL2/(32h).
Typically, L/2h=20, so the shear connection in the whole span has to resist a total shear force

Thus. This shear force is eight times the total load carried by the beam. A useful rule of thumb is that the strength of the shear connection for a beam is an order of magnitude greater than the load to be carried; it shows that shear connection has to be very strong.
In elastic design, the shear connectors are spaced in accordance with the shear flow. Thus, if the design shear resistance of a connector is p, is given by p·vx>pRD,. From equation (2.12) this is

This is known is triangular spacing from the shape of the graph of ν against x (Fig.2.4).