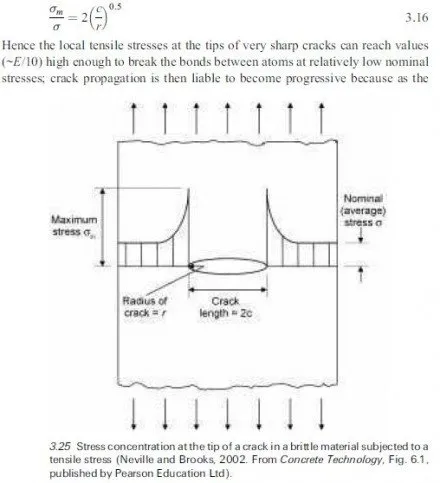
Linear elastic fracture mechanics is concerned with predicting conditions that give rise to rapid crack propagation in brittle materials that are considered to be elastic, homogeneous and isotropic at the onset of fracture; it involves the study of stress and displacement at the microscopic level in the region of a crack tip (Mindess and Young, 1981). The field developed from the pioneering work of Griffith (1920) who proposed criteria for the fracture of brittle solids that explained the discrepancy between their low observed bulk strengths and their much higher theoretical strengths (estimated for perfect crystals to be ~ E/10) by postulating the existence of microscopic flaws, which serve as stress concentrators. As illustrated in Figure 3.25, for an elliptical crack with dimensions as indicated, the maximum tensile stress near the crack tip is intensified by a factor that depends on the crack length and end radius according to the relationship:
crack length increases the maximum stress at the tip increases (equation 3.16) while the theoretical stress required to induce energetically favoured crack growth in a brittle material, stress f decreases in accordance with the following expression (Illston et al., 1979):
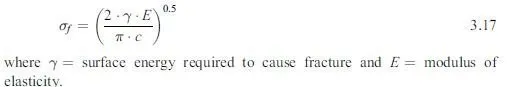
Similar reasoning has been used to explain the failure of concrete (Kaplan, 1961), which is generally regarded as being brittle with failure occurring at low strains due to linking of existing and newly-formed microcracks.
Strictly speaking, however, concrete exhibits some plasticity (non-linear stress-strain behaviour) prior to failure. It is also evidently heterogeneous as the properties of its constituents are not all identical and it develops a relatively large fracture zone due to microcracking which causes progressive softening of the material prior to complete failure. Various ways of incorporating the above effects into models of the fracture of concrete specimens of different sizes and shapes under different states of applied stress have been proposed and the application of non-linear fracture mechanics is believed to provide a more representative means of describing the fracture behaviour and ultimate capacity of concrete structures. Further consideration of this field is beyond the scope of the present chapter and readers who require more a detailed treatment are referred to specialist works such as the following (ACI SP-118, 1989; ACI Committee 446, 1991; Karihaloo, 1995; Shah et al., 1995).