Information on the properties of structural steel, concrete, and reinforcement is readily available.
Only that which has particular relevance to composite structures will be given here.
For the determination of the bending moments and shear forces in a beam or framed structure (known as global analysis) all three materials can be assumed to behave in a linear elastic manner, though an effective modulus has to be used for the concrete, to allow for its creep under sustained compressive stress. The effects of cracking of concrete in tension, and of shrinkage, can be allowed for, but are rarely significant in buildings.

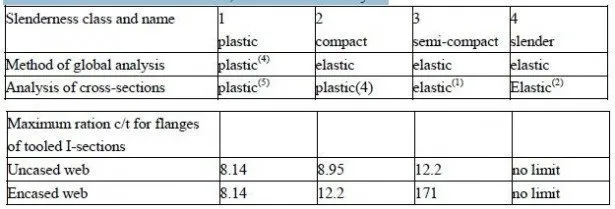
Rigid-plastic global analysis can sometimes be used (Section 4.3.3), despite the profound difference between a typical stress-strain curve for concrete in compression, and those for structural steel or reinforcement, in tension or compression, that is illustrated in Fig. 1.1. Concrete reaches its maximum compressive stress at a strain of between 0.002 and 0.003, and at higherstrains it crushes, losing almost all its compressive strength. It is very brittle in tension, having a strain capacity of only about 0.0001 (i.e. 0.1mm per metre) before it cracks. The figure also shows that the maximum stress reached by concrete in a beam or column is little more than 80% of its cube strength. Steel yields at a strain similar to that given for crushing of concrete, but on further straining the stress in steel continues to increase slowly, until the total strain is at least 40 times the yield strain. The subsequent necking and fracture is of significance for composite members only above internal supports of continuous beams, for the useful resistance of a cross-section is reached when all of the steel yields, when steel in compression buckles, or when concrete crushes. Resistances of cross-sections are determined (local analysis) using plastic analysis wherever possible, because results of elastic analyses are unreliable, unless careful account is taken of cracking, shrinkage, and creep of concrete, and also because plastic analysis is simpler and leads to more economical design.
The higher value of M γ that is used for concrete, in comparison with steel (Table 1.2) reflects not only the higher variability of the strength of test specimens, but also the variation in the strength of concrete over the depth of a member, due to migration of water before setting, and the larger errors in the dimensions of cross-sections, particularly in the positions of reinforcing bars. Brief comments are now given on individual materials.
Concrete
Reinforcing steel
Standard strength grades for reinforcing steel will be specified in EN 10 080 in terms of a characteristic yield strength fsk . Values of fsk used in worked examples here are 460 N/mm2, for ribbed bars, and 500N/mm2, for welded steel fabric or mesh. It is assumed here that both types of reinforcement satisfy the specifications for high bond action and high ductility to be given in
EN 10 080.
The modulus of elasticity for reinforcement, Es., is normally taken as 200 kN/mm2; but in a composite section it may be assumed to have the value for structural steel, E 210kN /mm2 a = , as the error is negligible.
Structural steel
Structural strength grades for structural steel are give in EN 10 025(17) in terms of a nominal yield strength fy and ultimate tensile strength fu . These values may be adopted as characteristic values in calculations. The grade used in worked examples here is S 355,f or which
![]()
for elements of all thicknesses up to 40 mm.
The density of structural steel is assumed to be 7850 kg/m3. Its coefficient of linear thermal expansion is given in Eurocode 3 as 12 ×10-6 per℃, but for simplicity the value 10×10-6per℃ (as??for reinforcement and normal-density concrete) may be used in the design of composite structures for buildings.
Profiled steel sheeting
This material is available with yield strengths (fyp) ranging from 235 N/mm2 to at least 460 N/mm2, in profiles with depths ranging from 45mm to over 200 mm, and with a wide range of shapes.
These include both re-entrant and open troughs, as in Fig. 3.9. These are various methods for achieving composite action with a concrete slab, discussed in Section 2.4.3.
Sheets are normally between 0.8mm and 1.5mm thick, and are protected from corrosion by a zine coating about 0.02mm thick on each face. Elastic properties of the material may be assumed to be as for structural steel.
Shear connectors
Details of these and the measurement of their resistance to shear are given in Chapter 2.