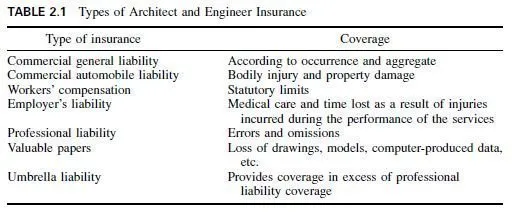
This process consists of:
1. Acoustical analysis
a. Determining the use of the structure the subjective needs
b. Establishing the desirable acoustical environment in each usable area
c. Determining noise and vibration sources inside and outside the structure
d. Studying the location and orientation of the structure and its interior spaces with regard to noise and noise sources
2. Acoustical design
a. Designing shapes, areas, volumes, and surfaces to accomplish what the analysis indicates
b. Choosing materials, systems, and constructions to achieve the desired result Sound and vibration sources are usually speech and sounds of normal human activity music, mechanical equipment sound and vibration, traffic, and the like.
Characteristics of these sound sources are well known or easily determined. Therefore, the builder or designer is usually most interested in the transmission paths for sound and vibration. These are gases (usually air); denser fluids (water, steam, oil, etc.); and solids (building materials themselves). During sound transmission in a
building, some of the sound energy is absorbed or dissipated, some is reflected from various surfaces, and some is transmitted through the building materials and furnishings.
Sound control is accomplished by means of barriers and enclosures, acoustically absorbent materials, and other materials and systems properly shaped and assembled.
Vibration control is accomplished by means of various resilient materials and assemblies, and by damping materials (viscoelastic materials of various types).
Airborne and structure-borne energy are controlled by somewhat different techniques, described in the following.
Airborne Sound Transmission
A sound source in a room sets the air into vibration. The vibrating air causes any barrier it touches (partitions, floors, ceilings, etc.) to vibrate. The vibrating barrier, in turn, sets into vibration the air on the opposite side of the barrier (Fig. 11.92).
The barrier, like any other body, resists motion because of its inherent inertia.
Because it takes more force, and therefore more energy, to move a heavier (more massive) barrier, sound loss through the barrier depends directly on the mass of the barrier. The loss in energy level between the original signal striking the barrier and the level of the energy transmitted to the opposite side is called the sound transmission loss of the barrier.
Figure 11.93 shows graphically how a truly limp barrier of infinite width and height responds to sound energy of varying frequency (the mass law, straight-line vibration). In practice, however, no barrier is truly limp; a wall, floor, or ceiling always has a finite stiffness. Therefore, at low frequencies, barriers tend to have higher sound transmission losses than the mass law predicts. In some region of the spectrum, however, barriers tend to have lower sound transmission losses (pass sound more readily) than the mass law indicates (see curve for solid panel in Fig. 11.93).


This latter phenomenon results because the barrier, in addition to its back-andforth motion, as shown in Fig. 11.92, moves in a simultaneous shear wave, like a rope being shaken (Fig. 11.90). At some frequency, the velocity of this shear wave in the barrier coincides with the velocity of the impinging sound wave in the air.
Then, the partition is quite transparent to sound, and a deep coincidence dip in the sound transmission loss curve occurs (see curve for double wall in Fig. 11.93). At frequencies above the coincidence frequency, the curve tends to recover its preceding slope.
There are few practical limp materials useful for ordinary building panels. Soft sheet lead is occasionally used for specialized barriers, as described in Art. 11.80, or is applied to other panel material to increase the mass of the composite without increasing its stiffness. In addition, damping materials (Art. 11.79.4) can be applied to the panels to damp out their vibrations quickly and to increase the energy loss as the panels vibrate.
Figure 11.93 shows another characteristic of barriers that further complicates their performance. While single, solid panels have somewhat smaller transmission losses than the mass law predicts, a double wall, a barrier comprising separated wythes or leaves, of the same total weight produces greater transmission losses than the mass law predicts.
If the mass of a single, solid panel is divided into two separate, unconnected layers, the only energy transfer between them occurs via the air between the layers.
Air is not stiff; it can sustain little of the shear wave, and it is not an efficient transmitter of the back-and-forth motion of one layer to the other (except at certain resonant frequencies). As a result, particularly in the midfrequencies, the sound transmission loss actually exceeds the mass-law values, often considerably. The greater the distance between layers, the better the performance. Theoretically, the sound transmission loss should increase about 6 dB for each doubling of the width of the airspace. In practice, however, the increase in decibels is somewhat less than this.
If a porous, sound-absorbent blanket is inserted in the void between layers, the standing waves in the air layers are minimized. Furthermore, such a blanket has the effect of reducing the stiffness of the air, as well as absorbing some of the energy of the air as it pumps back and forth through the blanket. The result is an additional increase in sound transmission loss.
The performance of various barriers, and rating systems for their performance, are shown in Table 11.27.