The following three methods are available for computation of volumes:
(i) From cross-sections (ii) From spot levels and
(iii) From contours.
First method is useful for computing earth work involved in road/rail/canal/sewage works. Second method is useful for finding earth work in foundations of large building and the last method is useful for finding capacity of reservoirs.
Computation of Volume from Cross-sections
To compute earth work, profile levelling is carried out along the centre line of the alignment of the project and cross-sectional levels are taken at regular intervals. Then the volume of earth work can be found, if the cross-sections are determined.
First the calculation of cross-sectional area is discussed.
(a) If section is level (Fig. 18.9)

Let h be the depth at the centre line of the alignment and 1 : n be the side slopes. Then
w = b + 2nh
∴ A = 1 /2 (w + b) h
= 1 / 2 (b + 2nh + b) h
= (b + nh) h
(b) If it is a multilevel section [Fig. 18.10]

Let the coordinates of points be (x1, y1), (x2, y2), …, (xn, yn), then arrange the coordinates in the following order

Then area of the figure
= 1 /2 [ Σ Product of pair of coordinates connected by continuous lines Σ Product of coordinates connected by dotted lines] …(18.9)
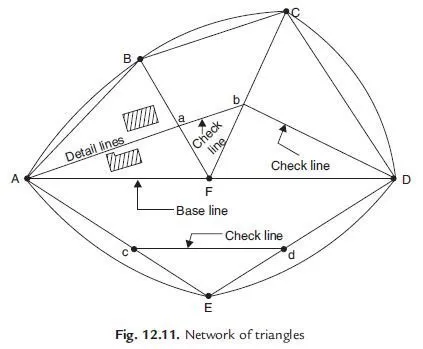
The above formula can be easily proved by taking a simple example of a quadrilateral [Ref. Fig.
18.11]. Let the coordinates of A, B, C and D be (x1, y1), (x2, y2), (x3, y3) and (x4, y4). Then area of ABCD = Area of a AB b + Area of b BC c + Area of c CD d Area of a AD d.
= 1 / 2 (x1+ x2) (y2 y1) + 1 / 2 (x2 + x3) (y3 y2) + 1 / 2 (x3 + x4) (y4 y3) 1 / 2 (x1 + x4) (y4 y1)

Calculation of Volumes
Once cross-sectional areas at various sections are known volume can be found from trapezoidal or prismoidal rule as given below:
Trapezoidal Rule
Prismoidal Rule

Computation of Earth Work from Spot Levels
This method is used to calculate volume of earth work for the elevations of basements, large tanks and borrow pits. In this method the whole area is divided into a number of rectangles or triangles (Fig. 18.13).
The levels are taken at corner points before and also after excavation. The depth of excavation at each corner point is measured. Then for each simple figure (rectangle or triangle).
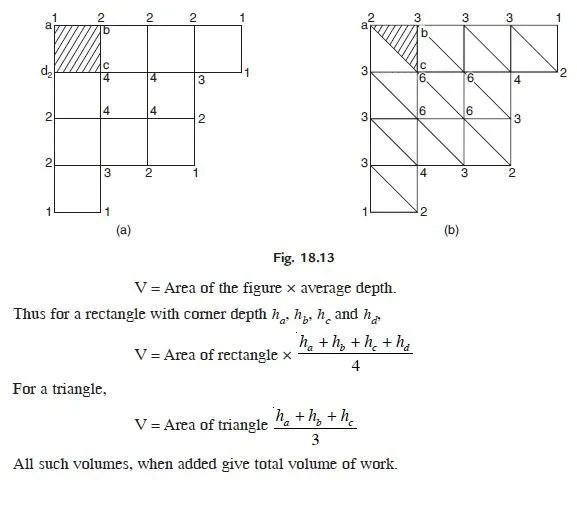
It may be noted that in Fig. 18.13 (a), in total volume calculations depth of some corners appear once, some twice, some of them 3 times and some 4 times. If
Σh1 = some of depths used once
Σh2 = sum of depths used twice
Σh3 = sum of depths used thrice
Σh4 = sum of depths used four times.
Then
Computation of Volume from Contours
Figure 18.15 shows a dam with full water level of 100 m and contours on upstream side. Capacity of reservoir to be found is nothing but volume of fill with water level at 100 m. The whole area lying within a contour line is found by planimeter. It may be noted that area to be measured is not between two consecutive contour lines.