If the area is bound by straight edges, it can be subdivided in a set of convenient figures and area calculated. But in most of the cases the boundary may have irregular shape. In such cases major area is subdivided into regular shape and area is found. The smaller area near the boundary is found from taking offset from a survey line [Ref. Fig. 18.1].

Computation of Areas of Regular Figures
The following expressions for calculating areas may be noted:

Areas of Irregular Shapes
For this purpose from a survey line offsets are taken at regular intervals and area is calculated from any one of the following methods:
(a) Area by Trapezoidal rule
(b) Area by Simpsons rule.
(a) Area by Trapezoidal Rule:
If there are n + 1 ordinates at n equal distances d, then total length of line is L = nd, Area of each segment is calculated treating it as a trapezium. Referring to Fig. 18.2,

Area by Simpsons Rule
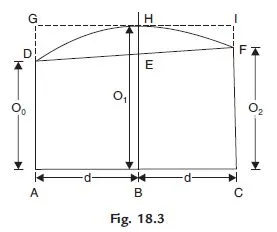
In this method, the boundary line between two segment is assumed parabolic. Figure 18.3 shows the first two segments of Fig. 18.2, in which boundary between the ordinates is assumed parabolic.
∴ Area of the first two segments
= Area of trapezium ACFD + Area of parabola DEFH
It is to be noted that the equation 18.6 is applicable if the number of segments (n) are even, in other words, if total number of ordinatess are odd.
If n is odd, then for n 1 segments area is calculated by Simpsons rule and for the last segment trapezoidal rule is applied.
Trapezoidal rule gives better results if the boundary is not irregular to great extent. Simpsons rule should be used if the boundary is highly irregular. This rule gives slightly more value compared to trapezoidal rule, if the curve is concave towards the survey line and gives lesser value, if the boundary is convex towards survey line.
In both methods accuracy can be improved if the number of segments are increased.