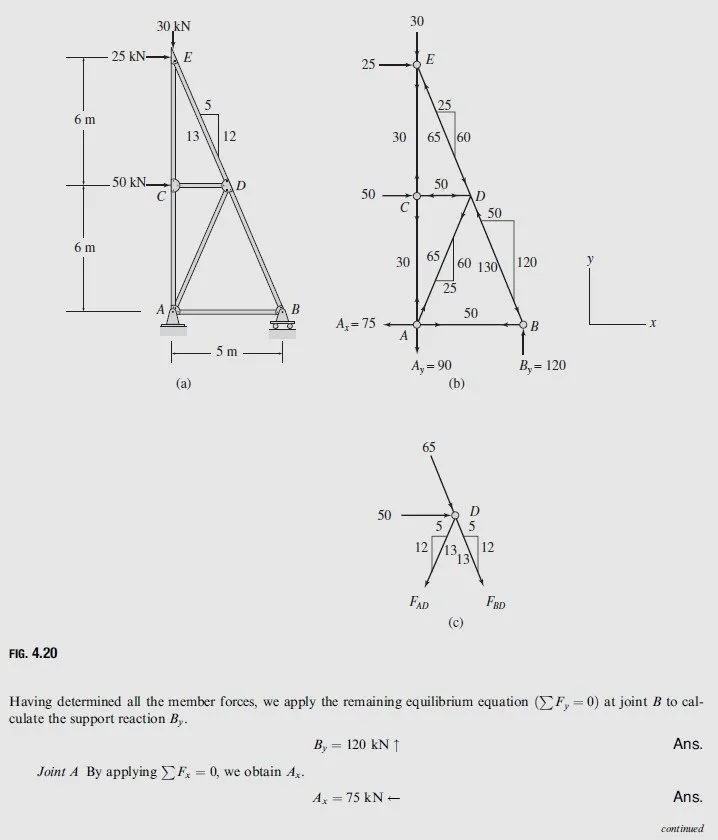
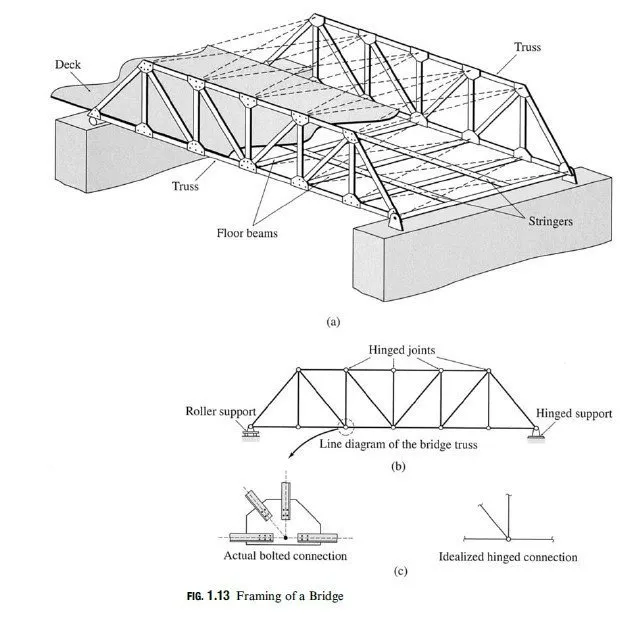
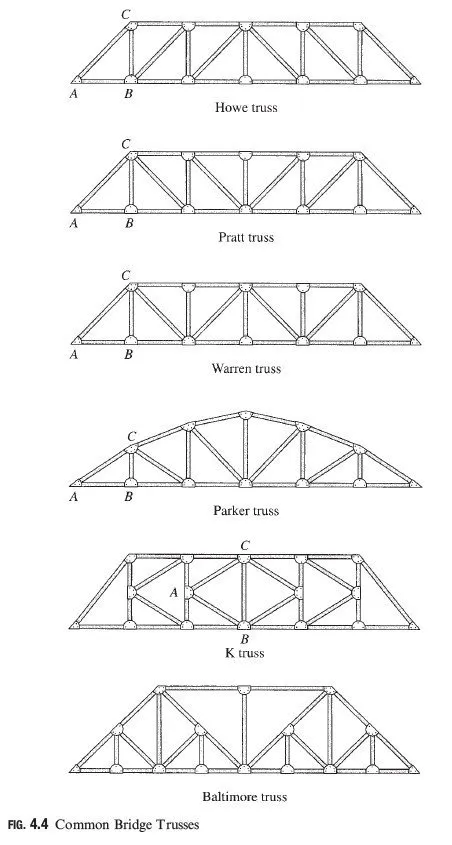
Example 4.5

Determine the force in each member of the truss shown in Fig. 4.20(a) by the method of joints. Solution Static Determinacy The truss is composed of 7 members and 5 joints and is supported by 3 reactions. Thus, m + r = 2j. Since the reactions and the members of the truss are properly arranged, it is statically determinate. From the dimensions of the truss given in Fig. 4.20(a), we find that all inclined members have slopes of 12:5. Since joint E has two unknown non-collinear forces, FCE and FDE, acting on it, we can begin the method of joints without first calculating the support reactions.

Joint E Focusing our attention on joint E in Fig. 4.20(b), we observe that in order to satisfy ∑Fx = 0, the horizontal component of FDE must push to the left into the joint with a magnitude of 25 kN to balance the 25 kN external load acting to the right. The slope of member DE is 12:5, so the magnitude of the vertical component of FDE is(12/5)(25) or 60 kN. Thus, the force in member DE is compressive, with a magnitude of

Example 4.6

Determine the force in each member of the three-hinged trussed arch shown in Fig. 4.21(a) by the method of joints. Solution Static Determinacy The truss contains 10 members and 7 joints and is supported by 4 reactions. Since m+r=2j  and the reactions and the members of the truss are properly arranged, it is statically determinate. Note that since m < 2j – 3, the truss is not internally stable, and it will not remain a rigid body when it is detached from its supports. However, when attached to the supports, the truss will maintain its shape and can be treated as a rigid body.

Zero-Force Members It can be seen from Fig. 4.21(a) that at joint C, three members, AC;CE, and CF, are connected, of which members AC and CF are collinear. Since joint C does not have any external load applied to it, the non-collinear member CE is a zero-force member.