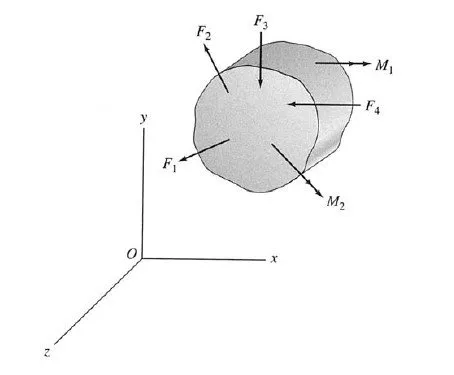
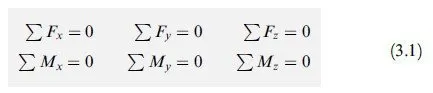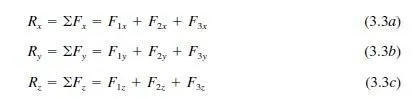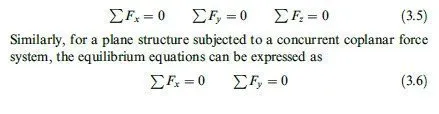A structure is considered to be in equilibrium if, initially at rest, it remains at rest when subjected to a system of forces and couples. If a structure is in equilibrium, then all its members and parts are also in equilibrium.
In order for a structure to be in equilibrium, all the forces and couples (including support reactions) acting on it must balance each other, and there must neither be a resultant force nor a resultant couple acting on the structure. Recall from statics that for a space (three-dimensional) structure subjected to three-dimensional systems of forces and couples (Fig. 3.1), the conditions of zero resultant force and zero resultant couple can be expressed in a Cartesian (xyz) coordinate system as
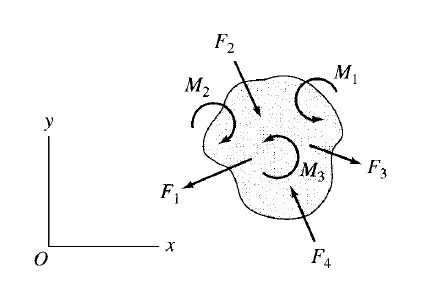
These six equations are called the equations of equilibrium of space structures and are the necessary and su°cient conditions for equilibrium. The first three equations ensure that there is no resultant force acting on the structure, and the last three equations express the fact that there is no resultant couple acting on the structure. For a plane structure lying in the xy plane and subjected to a coplanar system of forces and couples (Fig. 3.2), the necessary and su°- cient conditions for equilibrium can be expressed as
These three equations are referred to as the equations of equilibrium of plane structures. The first two of the three equilibrium equations express, respectively, that the algebraic sums of the x components and y components of all the forces are zero, thereby indicating that the resultant force acting on the structure i
s zero. The third equation indicates that the algebraic sum of the moments of all the forces about any point in the plane of the structure and the moments of any couples acting on the structure is zero, thereby indicating that the resultant couple acting on the structure is zero. All the equilibrium equations must be satisfied simultaneously for the structure to be in equilibrium. It should be realized that if a structure (e.g., an aerospace vehicle) initially in motion is subjected to forces that satisfy the equilibrium equations, it will maintain its motion with a constant velocity, since the forces cannot accelerate it. Such structures may also be considered to be in equilibrium. However, the term equilibrium is commonly used to refer to the state of rest of structures and is used in this context herein.
Alternative Forms of Equations of Equilibrium of Plane Structures
Although the equilibrium equations as expressed in Eq. (3.2) provide the most convenient means of analyzing a majority of plane structures, the analysis of some structures can be expedited by employing one of the following two alternative forms of the equations of equilibrium:
in which A; B, and C are any points in the plane of the structure, provided that these three points do not lie on the same straight line.
Concurrent Force Systems
When a structure is in equilibrium under the action of a concurrent force system that is, the lines of action of all the forces intersect at a single point the moment equilibrium equations are automatically satisfied, and only the force equilibrium equations need to be considered.
Therefore, for a space structure subjected to a concurrent threedimensional
force system, the equations of equilibrium are
Two-Force and Three-Force Structures
Throughout this text, we will encounter several structures and structural members that will be in equilibrium under the action of only two, or three, forces. The analysis of such structures and of structures composed of such members can be considerably expedited by recalling from statics the following characteristics of such systems:
1. If a structure is in equilibrium under the action of only two forces, the forces must be equal, opposite, and collinear.
2. If a structure is in equilibrium under the action of only three forces, the forces must be either concurrent or parallel.