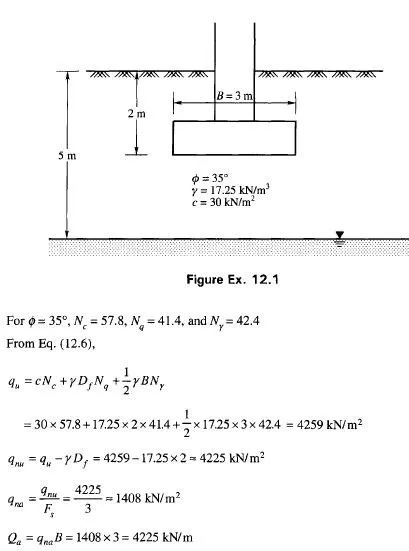
Section AB in Fig. 11.6(a) in a semi-infinite mass is replaced by a smooth wall AB in Fig. 11.7(a).
The lateral pressure acting against smooth wall AB is due to the mass of soil ABC above failure line AC which makes an angle of 45° + 0/2 with the horizontal. The lateral pressure distribution on wall AB of height H increases in simple proportion to depth. The pressure acts normal to the wall AB [Fig. 11.7(b)].
The lateral active pressure at A is
The total pressure on AB is therefore

Backfill Horizontal-Passive Earth Pressure
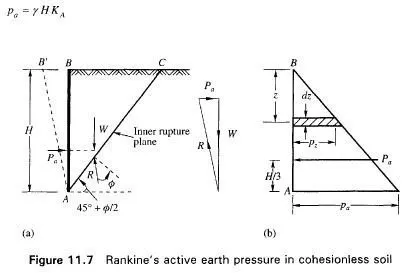
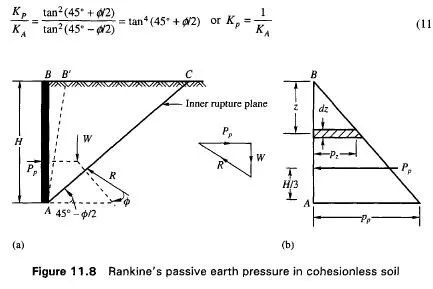
If wall AB is pushed into the mass to such an extent as to impart uniform compression throughout the mass, soil wedge ABC in Fig. 11.8(a) will be in Rankine’s passive state of plastic equilibrium. The inner rupture plane AC makes an angle 45° + 0/2 with the vertical AB. The pressure distribution on wall AB is linear as shown in Fig. 11.8(b).
The passive pressure p at A is

Relationship between Kp and KA
The ratio of Kp and KA may be written as
This simple demonstration indicates that the value of Kp is quite large compared to KA.
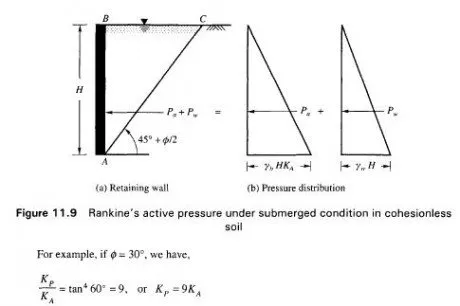
Active Earth Pressure-Backfill Soil Submerged with the Surface Horizontal
When the backfill is fully submerged, two types of pressures act on wall AB. (Fig. 1 1.9) They are
1. The active earth pressure due to the submerged weight of soil
2. The lateral pressure due to water
At any depth z the total unit pressure on the wall is

Active Earth Pressure-Backfill Partly Submerged with a Uniform Surcharge Load
The ground water table is at a depth of Hl below the surface and the soil above this level has an effective moist unit weight of y. The soil below the water table is submerged with a submerged unit weight yb. In this case, the total unit pressure may be expressed as given below.
At depth Hl at the level of the water table

Sloping Surface-Active Earth Pressure
Figure 1 1.1 1 (a) shows a smooth vertical wall with a sloping backfill of cohesionless soil. As in the case of a horizontal backfill, the active state of plastic equilibrium can be developed in the backfill by rotating the wall about A away from the backfill. Let AC be the rupture line and the soil within the wedge ABC be in an active state of plastic equilibrium. Consider a rhombic element E within the plastic zone ABC which is shown to a larger scale outside. The base of the element is parallel to the backfill surface which is inclined at an angle /3 to the horizontal. The horizontal width of the element is taken as unity. Let o~v = the vertical stress acting on an elemental length ab = (7l = the lateral pressure acting on vertical surface be of the element The vertical stress o~v can be resolved into components <3n the normal stress and t the shear stress on surface ab of element E. We may now write