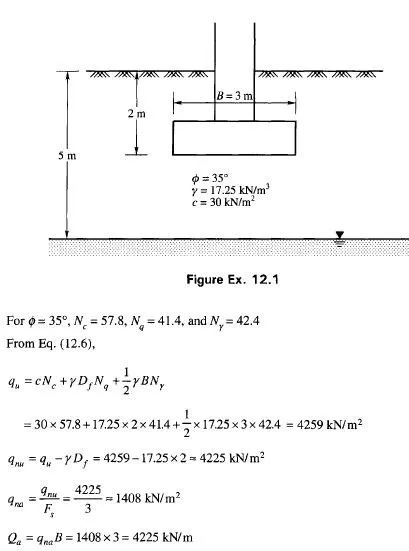
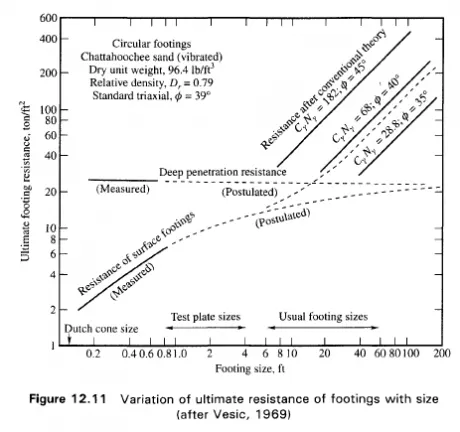
Terzaghi (1943) developed Eq. (12.6) based on the assumption that the soil is incompressible. In order to take into account the compressibility of soil, he proposed reduced strength characteristics c and 0 defined by Eq. (12.11). As per Vesic (1973) a flat reduction of 0 in the case of local and punching shear failures is too conservative and ignores the existence of scale effects. It has been conclusively established that the ultimate bearing capacity qu of soil does not increase in proportion to the increase in the size of the footing as shown in Fig. 12.11 or otherwise the bearing capacity factor Af decreases with the increase in the size of the footing as shown in Fig. 12.12. In order to take into account the influence of soil compressibility and the related scale effects, Vesic (1973) proposed a modification of Eq. (12.27) by introducing compressibility factors as follows.


Eq. (12.29) was developed on the basis of the theory of expansion of cavities in an infinite solid with the assumed ideal elastic properties behavior of soil. In order to take care of the volumetric strain A in the plastic zone, Vesic (1965) suggested that the value of Ir, given by Eq. (12.29), be reduced by the following equation.

It is known that Ir varies with the stress level and the character of loading. A high value of Irr, for example over 250, implies a relatively incompressible soil mass, whereas a low value of say 10 implies a relatively compressible soil mass.
Based on the theory of expansion of cavities, Vesic developed the following equation for the compressibility factors.

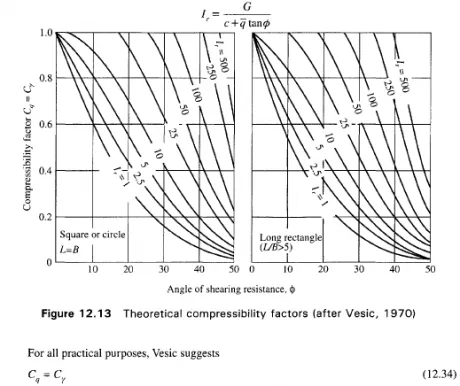
Equations (12.30) through Eq. (12.34) are valid as long as the values of the compressibility factors are less than unity. Fig. 12.13 shows graphically the relationship between C (= C ) and 0 for two extreme cases ofL/B > 5 (strip footing) and B/L = 1 (square) for different values of Ir (Vesic 1970). Vesic gives another expression called the critical rigidity index (Ir)cr expressed as
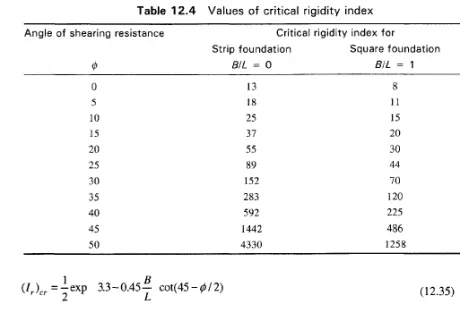
The magnitude of (I)cr for any angle of 0 and any foundation shape reduces the bearing capacity because of compressibility effects. Numerical values of (l)cr for two extreme cases ofB/L = 0 and BIL = 1 are given in Table 12.4 for various values of 0.
The concept and analysis developed above by Vesic (1973) are based on a limited number of small scale model tests and need verification in field conditions.