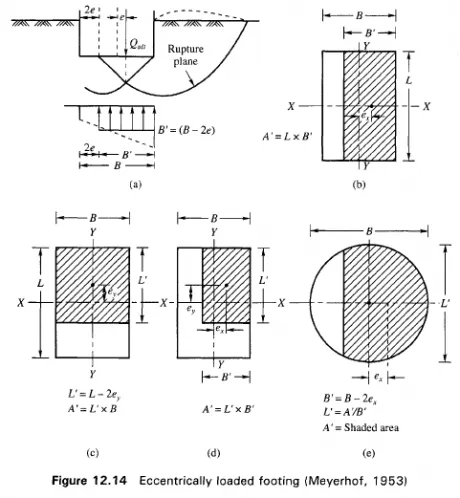
Foundations Subjected to Eccentric Vertical Loads If a foundation is subjected to lateral loads and moments in addition to vertical loads, eccentricity in loading results. The point of application of the resultant of all the loads would lie outside the geometric center of the foundation, resulting in eccentricity in loading. The eccentricity e is measured from the center of the foundation to the point of application normal to the axis of the foundation. The maximum eccentricity normally allowed is B/6 where B is the width of the foundation. The basic problem is to determine the effect of the eccentricity on the ultimate bearing capacity of the foundation. When a foundation is subjected to an eccentric vertical load, as shown in Fig. 12.14(a), it tilts towards the side of the eccentricity and the contact pressure increases on the side of tilt and decreases on the opposite side. When the vertical load Qult reaches the ultimate load, there will be a failure of the supporting soil on the side of eccentricity. As a consequence, settlement of the footing will be associated with tilting of the base towards the side of eccentricity. If the eccentricity is very small, the load required to produce this type of failure is almost equal to the load required for producing a symmetrical general shear failure. Failure occurs due to intense radial shear on one side of the plane of symmetry, while the deformations in the zone of radial shear on the other side are still insignificant. For this reason the failure is always associated with a heave on that side towards which the footing tilts.
Research and observations of Meyerhof (1953, 1963) indicate that effective footing dimensions obtained (Fig. 12.14) as

Determination of Maximum and Minimum Base Pressures Under Eccentric Loadings
The methods of determining the effective area of a footing subjected to eccentric loadings have been discussed earlier. It is now necessary to know the maximum and minimum base pressures under the same loadings. Consider the plan of a rectangular footing given in Fig. 12.15 subjected to eccentric loadings.
Let the coordinate axes XX and YY pass through the center O of the footing. If a vertical load passes through O, the footing is symmetrically loaded. If the vertical load passes through Ox on the X-axis, the footing is eccentrically loaded with one way eccentricity. The distance of Ox from O, designated as ex, is called the eccentricity in the X-direction. If the load passes through O on the 7-axis, the eccentricity is e in the F-direction. If on the other hand the load passes through 0 the eccentricity is called two-way eccentricity or double eccentricity.
When a footing is eccentrically loaded, the soil experiences a maximum or a minimum pressure at one of the corners or edges of the footing. For the load passing through O (Fig. 12.15), the points C and D at the corners of the footing experience the maximum and minimum pressures respectively.


When ex or e exceed a certain limit, Eq. (12.39) gives a negative value of q which indicates tension between the soil and the bottom of the footing. Eqs (12.39) are applicable only when the load is applied within a limited area which is known as the Kern as is shown shaded in Fig 12.15 so that the load may fall within the shaded area to avoid tension. The procedure for the determination of soil pressure when the load is applied outside the kern is laborious and as such not dealt with here. However, charts are available for ready calculations in references such as Teng (1969) and Highter and Anders (1985).