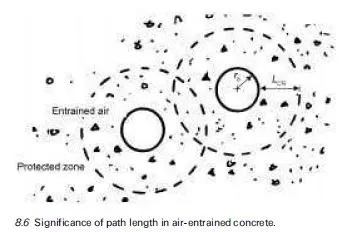
The freezing point of a liquid is a function of temperature and pressure. The pore structure of concrete includes a wide range of diameters (see Chapter 2) and this influences the freezing phenomenon. Ice formation begins in the coarsest capillary pores while water in the adjacent gel pores within C-S-H initially remains unfrozen. There is a thermodynamic relationship between freezing point and pore radius because the surface energy of the pore walls leads to adsorption of water molecules and so to a depression in the freezing point through a reduction of the pore water’s chemical potential. A thin film of adsorbed water at the pore surface remains unfrozen even after ice is formed in the pore and, the greater the specific surface of the pores, the more the freezing point is depressed. Pores with a radius of 5 nm or less could remain unfrozen in temperatures above ÿ20ëC and only two-thirds of the pore water may be frozen by ÿ60ëC (see for example Sellevold and Bager, 1980; Pigeon and Pleau, 1995; Comite Euro- International du Beton, 1989).
Given the extensive nature of the C-S-H component of hydrated cement and its ultra-fine pore structure (see Chapter 2 and Powers, 1958) it is consequently possible that temperatures could fall to ÿ30ëC and less than half of the pore water in a typical example of concrete might be frozen. Issues of significance are the degree of saturation, the ability of the concrete to facilitate enforced movement of unfrozen water and accommodate the growth of ice bodies. Growth of an ice body requires a seed ice crystal. Water may become supercooled if a seed crystal does not exist. Thus there are many factors to account for the variability in the phenomenon of conversion of water to ice in concrete at subzero temperatures. Indeed Stark and Ludwig (1997) have demonstrated that water quality has a considerable influence on the frost resistance of concrete.