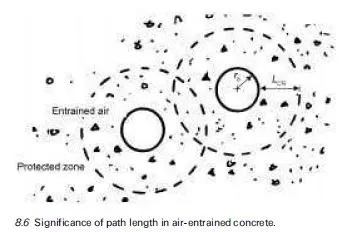
The definition of pure elasticity is that strains appear and disappear on application and removal of stress. The elastic properties of engineering materials fall into four categories, as illustrated in Fig. 3.1, which show two categories of pure elasticity: (a) linear and elastic and (b) non-linear and elastic. In both cases, the ascending curve coincides with the descending curve. The other two categories are: (c) linear and non-elastic and (d) non-linear and non-elastic, where the ascending and descending curves are separate so that after removal of load there is a permanent strain or deformation. The area enclosed by the two curves is termed hysteresis, which represents the energy absorbed by the material due to the damage caused by loading. In the case of concrete, the hysteresis is due mainly to microcracking at the aggregate-cement paste inter- face and irreversible creep, its magnitude depending on the age of the concrete and especially the rate of loading. An increase in age or maturity reduces the hysteresis, while very rapid loading reduces the curvature of the stress-strain behaviour and hysteresis considerably. The slope of the stress-strain curve gives the modulus of elasticity, known generally as Young’s modulus. Whereas for steel the slope is constant, for concrete it can be seen that the modulus varies according to the level of stress (as well as rate of loading and age) and whether the load is increasing or decreasing. The various types of modulus used to describe the elastic behaviour of concrete are fully detailed elsewhere (Neville, 1995; Neville and Brooks, 2002). When the load is applied for the first time to a particular level, the secant modulus yields the strain response and the starting point for creep, if the load is subsequently sustained. In a creep test, the strain on application of load is termed the elastic strain at loading and the time of application of load should always be stated. Repeating the cycles of loading and unloading reduces the hysteresis so that the ascending and descending stress-strain curves eventually coincide andbecome approximately linear.

This procedure is the basis of standard methods of test for the determination of the static modulus of elasticity such as ASTM C469- 94 and BS 1881: Part 121:1983. The modulus of elasticity generally follows the pattern of strength, although not always. For example, wet concrete tends to have a greater modulus than dry concrete, while strength varies in the opposite sense. The type of aggregate can also be different in its effect on modulus and strength. However, for design purposes, most Codes of Practice give empirical relationships between modulus and strength. Generally, with normal weight concrete of density, P 2320 kg/m3 the static modulus, Ec (GPa), can be related to the cube compressive strength, fcu (MPa), by the expression:
The influence of aggregate on modulus of elasticity of concrete has already been mentioned, the two-fold effect arising from the stiffness (modulus) of the aggregate and its volumetric proportion in concrete. The stiffer the aggregate, the greater the modulus of concrete and, for aggregate having a greater modulus than hardened cement paste, the greater the volume of aggregate the greater the modulus of concrete. The modulus of elasticity of lightweight aggregate con- crete is usually between 40 and 80% of the modulus of normal weight concrete of the same strength, the mix proportions having little influence. The relationships between modulus of elasticity and compressive strength (equations 3.1±3.4) are not appreciably different when either chemical or mineral admixtures are used to make concrete (Brooks, 1999).