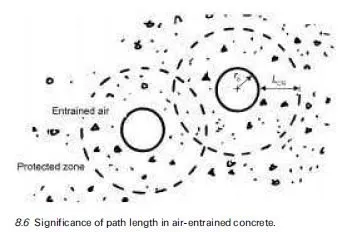
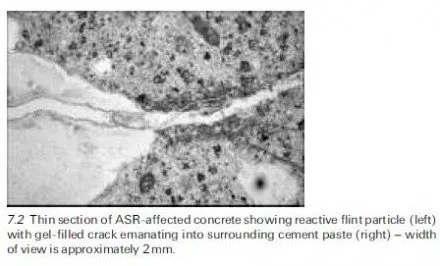
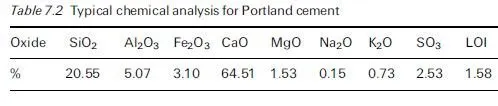
As far as new reinforced concrete structures are concerned, most modern codes of practice have adopted strict limits on maximum levels of chloride permitted in concreting materials, so future corrosion problems arising purely from this source should be rare as long as carbonation does not penetrate through the cover concrete. Avoidance of excessive carbonation is of course necessary because even relatively low levels of chloride in carbonated concrete have been found to exacerbate the corrosion rate of embedded steel significantly (Glass et al., 1991). In cases where carbonation is unlikely to pose any real threat, however, there remains a problem of how to avoid chloride-induced corrosion for structures exposed to external chlorides derived from seawater or deicing salts. Research into factors that determine the rates of penetration of chloride ions into concrete has therefore been a topic of worldwide activity and, in recent years, a series of international workshops on this subject has been held (RILEM, 1997, 2000, 2005).
As was noted in Chapter 2, the means by which ions penetrate into concrete (and/or may be removed from it) are often complex and dependent to a large extent on the moisture condition of the material at the time of exposure. To describe the various processes involved in reasonable detail, even assuming idealised initial and boundary conditions apply, would require consideration of several different types of transport mechanism (diffusion, convection/capillary suction and migration) coupled with the effects of ion/ion and ion/pore surface interactions. Such a treatment is beyond the scope of the present chapter and the primary focus here will be on more immediately pragmatic issues. Essentially we need to consider how adequately, or otherwise, current knowledge enables us to model chloride ingress into concrete with a view to predicting corrosion initiation times in reinforced concrete with reasonable accuracy.
In a recent review, Buenfeld (2004) has classified models for predicting deterioration of concrete under three headings, viz. empirical, semi-empirical and mechanistic. Mechanistic models are categorised as those which mathe- matically represent individual transport processes and chemical reactions, based on measurable coefficients, and combine their effects to make an overall prediction. Semi-empirical models are described as those which relate deterioration to what are loosely referred to as `quasi-transport’ coefficients, largely dependent on concrete properties (but representing the combined effects of transport processes, chemical reactions, exposure time, etc.). Empirical models are those that base their predictions purely on previously observed behaviour without consideration of the processes involved in bringing about deterioration.
With the widespread availability of low-cost computing, there has been growing interest in developing mechanistic approaches to modelling of the transport of chloride (and other ions) in hardened concrete exposed under various conditions, see for example (Truc, 2000; Marchand, 2001; Johannesson, 2003; Wang et al., 2005). These usually make use of modified forms of the Nernst-Planck equation, which is a general expression for the mass transfer of ions in very dilute electrolytes (Bard and Faulkner, 1980), to represent the fluxes (Ji) of the various ionic species present in the concrete pore electrolyte in terms of their individual diffusion coefficients (Di), concentrations (Ci), and charge numbers (zi). The approach was originally applied by Yu (1990) in an attempt to simulate the results of some earlier experimental investigations of diffusion of several ions (Na+, Clÿ, OHÿ) in hardened cement paste specimens, which had been exposed to a salt solution and subjected to detailed pore solution analyses at various positions along the diffusion path (Sergi, 1986).
The provision of adequate experimental data to validate such `multi-species’ models, however, is generally problematic and some of the `measurable’ coefficients they incorporate are very difficult to estimate with reasonable confidence. These include, the activity coefficients of individual species in mixed electrolytes of high ionic strength and coefficients involved in `binding isotherm’ relationships between free and bound ionic concentrations, etc. To date, empirical or semi-empirical, models have therefore been more commonly employed and the most widely (but not always appropriately) used service-life model of any type has been based on a standard analytical solution of Fick’s second law of diffusion, a partial differential equation relating the temporal and spatial variations in concentration (C) of the diffusing substance via a `diffusion coefficient’ (D)1 (Crank, 1975). The solution concerned is commonly known as the `error function’ equation and the form in which it has often been applied for the prediction of unidirectional chloride penetration into concrete, is expressed

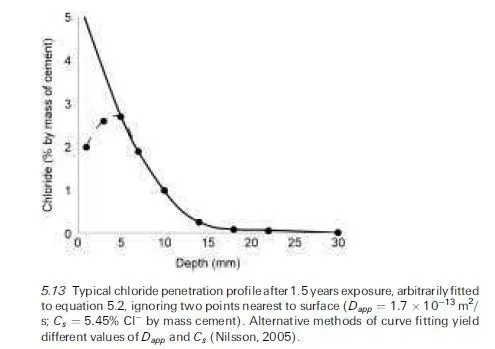
The prefix `apparent’, as used here and previously elsewhere (Sergi et al., 1991) in the term `apparent diffusion coefficient’ (Dapp), should be noted because its meaning (i.e., seeming, as distinct from real) is important. It reflects the fact that Dapp is neither a basic material property, nor even purely a measure of diffusion resistance for concrete in a specific environment. It is merely a regression parameter obtained by arbitrarily fitting measured chloride pene- tration profiles in concrete to equation 5.2, as illustrated in Fig. 5.13. It is worth emphasising this point because there has been confusion in the literature regarding the terminology employed in this context by different authors and some misunderstanding of the distinction between Dapp and other transport coefficients, e.g. those obtained from steady-state chloride diffusion measure- ments, designated `effective diffusion coefficients’ (Page et al., 1981). A discussion of relationships between various forms of `diffusion coefficient’ that have been used to characterise chloride transport in concrete is provided by Tang (1996) and a clear demonstration of the wide variations in calculated values of the regression parameters, Dapp and Cs, that can arise when various arbitrarily chosen curve fitting procedures are applied to a given set of chloride ingress data, is presented by Nilsson (2005).
With regard to the use of `apparent diffusion coefficients’, it should also be recognised that the error function solution of Fick’s second law was derived for unidirectional diffusion (under constant assumed initial and boundary conditions) of an uncharged substance into a semi-infinite slab of material for which the diffusion coefficient was assumed to be independent of both time and depth (Crank, 1975). Chloride penetration into concrete is never a simple process of this type because, even if the material is fully saturated from the outset (not often the case in reality) and its properties are assumed not to vary significantly with time or depth (highly improbable in practice), chloride ions are negatively charged particles, so their movement is always coupled to the transport of other ions; also some of the chloride ions that enter the concrete interact with, and become bound chemically and/or physically by, solid hydration products of the cement. Thus the `apparent diffusion coefficient’ may be regarded as a `quasi-transport’ coefficient, which is dependent not only on what Diamond in Chapter 2 calls the `permeation capacity’ of concrete but also on its `chloride binding capacity’. As far as ionic diffusion is concerned, the `permeation capacity’ depends largely on the continuity and tortuosity of the coarser pores within the material and, from simple analysis of steady state chloride diffusion data, it would appear that chloride ions are not transported at significant rates through hydrated cement pastes unless pores wider than about 30 nm are present (Ngala and Page, 1997).
In spite of the fundamental objections that can be raised to using `quasi- transport’ coefficients such as Dapp to describe chloride penetration into con- crete, they have now been employed in this context by many authors for several decades. This follows from early research on the penetration of deicing salts into cement pastes and concrete (Collepardi et al., 1972) and even earlier investi- gations of the diffusion of several radioactively labelled anions and cations into hydrated cements (Spinks et al., 1952), where the error function solution to Fick’s second law was applied. They have commonly been used in service-life prediction models, often incorporating empirical corrections that are intended to rectify some of the obvious discrepancies that appear when measured chloride penetration profiles are interpolated to equation 5.2. Thus, for instance, deviations from the error function relationship that are often observed near the externally exposed surface of concrete (see Fig. 5.13) have been dealt with either by ignoring data from this region and extrapolating the best-fit curve to the remaining points to yield values for Dapp and an `apparent’ surface chloride content (cs) or by other arbitrary methods. Similarly, the fact that measured values of Dapp are not constant for a given type of concrete, but show markedtime-dependency (particularly so for concretes made from blended and composite cementitious binders that develop increasing diffusion resistance over very long periods in moist environments), has been dealt with by intro- ducing an empirical `time-dependent apparent diffusion coefficient’ (Dapp…t†) into equation 5.2; this is usually expressed by a relationship of the following form (Mangat and Molloy, 1994; Bamforth, 2004):

While this would appear to provide a straightforward method of accounting for differences in the rates of microstructure development and evolution of chloride penetration resistance for different types of concrete, detailed methods of determining values of n are not yet well established. As demonstrated in a recent investigation that examined three such current methods, this can lead to major variability in service-life predictions that are based on the various measured n values (Nokken et al., 2006). The requirement for long-term data to be available to provide credible information about `age factors’ is therefore obvious. It is also relevant to note that such data need to have been acquired under reasonably realistic conditions of moisture history as different types of concrete are liable to show different sensitivity to this variable, something that may be reflected in their long-term resistance to chloride penetration. The nature and properties of the C-S-H phases in different cementitious binder systems vary substantially (Taylor, 1997) and there is concern that the enhanced susceptibility to early-age cracking of some types of very low water/cement ratio concrete incorporating certain types of blended or composite cement may adversely affect their durability (Shah and Weiss, 2000). This is one of the main areas where further research is needed as the poorly defined relationships that often exist between crack distribution, crack width, cover depth and severity of chloride- induced corrosion of embedded steel in concrete of different types has generated extensive debate but basic understanding has not proved easy to achieve (Darwin et al., 1985; Schiessl and Raupach, 1997).
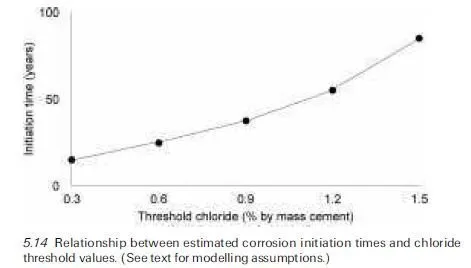
Another area of evident research need is related to the development of effective ways of reducing current uncertainty regarding chloride threshold levels for different types of concrete under different exposure conditions because of the sensitivity of predicted service lives to the assumed chloride threshold value (Ccrit). Thus, if the error function solution of Fick’s second law (equation 5.2) is used to estimate chloride penetration profiles for concrete with stipulated values of, say, Dapp ˆ 10ÿ12 m2/s, Cs ˆ 2% Clÿ by mass of cement, Ci ˆ 0% Clÿ by mass of cement, the corrosion initiation time (t0) varies as a function of the
In concluding this section, it is suggested that there are good reasons for caution when applying current methodologies for prediction of the initiation time for corrosion of steel in concrete exposed to the most severe chloride environments (Andrade et al., 2005). Partly this is due to lack of rigorous mechanistic models of chloride ingress validated by adequate data but, perhaps even more importantly, to current uncertainties regarding chloride threshold levels. Useful progress has been made, nevertheless, in developing improved guidance for specification of reinforced concrete suited for different chloride environments corresponding to the exposure classes described in the European standard BS EN 206 and complementary national standards such as BS 8500. These classes are as designated in Tables 5.1(b) and (c) and the rationale for corresponding limiting values of nominal cover, minimum cement content, and maximum water/cement ratio, applicable to reinforced concrete made with various cementitious binders, has been discussed by several authors (Hobbs and Matthews, 1998; Hobbs, 2001; Richardson, 2002; Thomas and Matthews, 2004). In BS 8500, the recommendations on limiting values for reinforced concrete exposed to a risk of chloride-induced corrosion (XD and XS exposures) are for an intended working life of at least 50 years. This standard gives no precise recommendations for an intended working life of at least 100 years in XD and XS exposures because, as it states, the spread of data from research and surveys of actual structures indicate that understanding of the processes involved is not yet adequate to produce such recommendations.