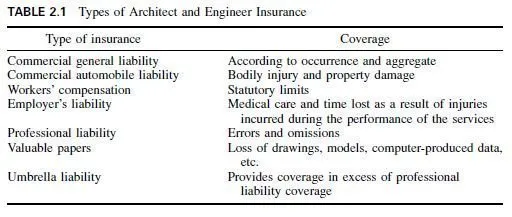
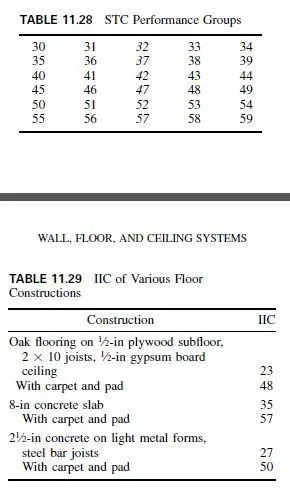
A force may be represented by a straight line of fixed length. The length of line to a given scale represents the magnitude of the force. The position of the line parallels the line of action of the force. And an arrowhead on the line indicates the direction in which the force acts.
Forces are concurrent when their lines of action meet. If they lie in the same plane, they are coplanar.
Parallelogram of Forces
The resultant of several forces is a single forces that would produce the same effect on a rigid body. The resultant of two concurrent forces is determined by the parallelogram law:
If a parallelogram is constructed with two forces as sides, the diagonal represents the resultant of the forces (Fig. 5.45a).
The resultant is said to be equal to the sum of the forces, sum here meaning, of course, addition by the parallelogram law. Subtraction is carried out in the same manner as addition, but the direction of the force to be subtracted is reversed.
If the direction of the resultant is reversed, it becomes the equilibrant, a single force that will hold the two given forces in equilibrium.
Resolution of Forces
To resolve a force into two components, a parallelogram is drawn with the force as a diagonal. The sides of the parallelogram represent the components. The procedure is: (1) Draw the given force. (2) From both ends of the force draw lines parallel to the directions in which the components act. (3) Draw the components along the parallels through the origin of the given force to the intersections with the parallels through the other end. Thus, in Fig. 5.45a, P1 and P2 are the components in directions OA and OB of the force represented by OC.
Force Polygons
Examination of Fig. 5.45a indicates that a step can be saved in adding the two forces. The same resultant could be obtained by drawing only the upper half of the parallelogram. Hence, to add two forces, draw the first force; then draw the second force beginning at the end of the first one. The resultant is the force drawn from the origin of the first force to the end of the second force, as shown in Fig. 5.45b.
Again, the equilibrant is the resultant with direction reversed.
From this diagram, an important conclusion can be drawn: If three forces meeting at a point are in equilibrium, they will form a closed force triangle.
The conclusions reached for addition of two forces can be generalized for several concurrent forces: To add several forces, P1, P2, P3, . . . , Pn, draw P2 from the end of P1, P3 from the end of P2, etc. The force required to close the force polygon is the resultant (Fig. 5.45c).
If a group of concurrent forces are in equilibrium, they will form a closed force polygon.