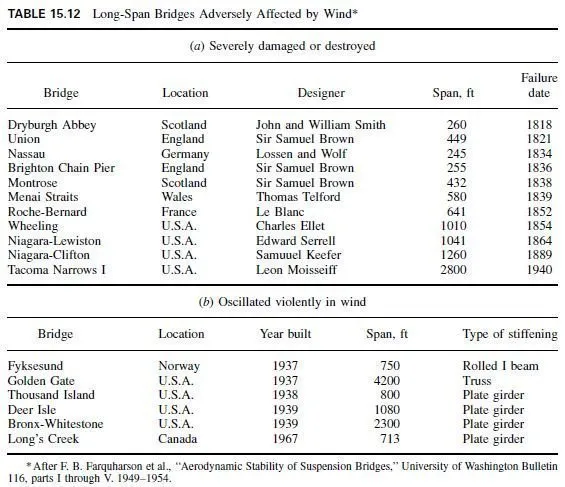
Because of the many strength levels and grades now available, designers usually must investigate several steels to determine the most economical one for each application. As a
guide, relative material costs of several structural steels used as tension members, beams, and columns are discussed below. The comparisons are based on cost of steel to fabricators (steel producers price) because, in most applications, cost of a steel design is closely related to material costs. However, the total fabricated and erected cost of the structure should be considered in a final cost analysis. Thus the relationships shown should be considered as only a general guide.
Tension Members. Assume that two tension members of different-strength steels have the same length. Then, their material-cost ratio C2 /C1 is
![]()
where A1 and A2 are the cross-sectional areas and p1 and p2 are the material prices per unit weight. If the members are designed to carry the same load at a stress that is a fixed percentage of the yield point, the cross-sectional areas are inversely proportional to the yield stresses. Therefore, their relative material cost can be expressed as
![]()
where Fy1 and Fy2 are the yield stresses of the two steels. The ratio p2 /p1 is the relative price factor. Values of this factor for several steels are given in Table 1.4, with A36 steel as the base. The table indicates that the relative price factor is always less than the corresponding yield-stress ratio. Thus the relative cost of tension members calculated from Eq. (1.2) favors the use of high-strength steels.
Beams. The optimal section modulus for an elastically designed I-shaped beam results when the area of both flanges equals half the total cross-sectional area of the member.
Assume now two members made of steels having different yield points and designed to carry the same bending moment, each beam being laterally braced and proportioned for optimal
section modulus. Their relative weight W2 /W1 and relative cost C2 /C1 are influenced by the web depth-to-thickness ratio d/ t. For example, if the two members have the same d/ t values, such as a maximum value imposed by the manufacturing process for rolled beams, the relationships are
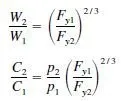
If each of the two members has the maximum d/ t value that precludes elastic web buckling, a condition of interest in designing fabricated plate girders, the relationships are
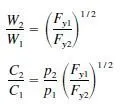
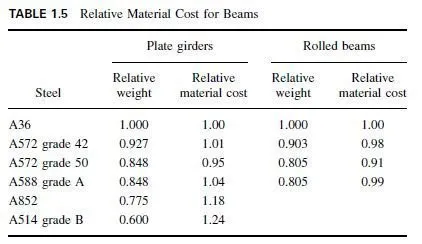
Table 1.5 shows relative weights and relative material costs for several structural steels. These values were calculated from Eqs. (1.3) to (1.6) and the relative price factors given in Table 1.4, with A36 steel as the base. The table shows the decrease in relative weight with increase in yield stress. The relative material costs show that when bending members are thus compared for girders, the cost of A572 grade 50 steel is lower than that of A36 steel, and the cost of other steels is higher. For rolled beams, all the HSLA steels have marginally lower relative costs, and A572 grade 50 has the lowest cost.
Because the comparison is valid only for members subjected to the same bending moment, it does not indicate the relative costs for girders over long spans where the weight of the member may be a significant part of the loading. Under such conditions, the relative material costs of the stronger steels decrease from those shown in the table because of the reduction in girder weights. Also, significant economies can sometimes be realized by the use of hybrid girders, that is, girders having a lower-yield-stress material for the web than for the flange.
HSLA steels, such as A572 grade 50, are often more economical for composite beams in
the floors of buildings. Also, A588 steel is often preferred for bridge members in view of its greater durability.
Columns. The relative material cost for two columns of different steels designed to carry the same load may be expressed as
where Fc1 and Fc2 are the column buckling stresses for the two members. This relationship is similar to that given for tension members, except that buckling stress is used instead of yield stress in computing the relative price-strength ratios. Buckling stresses can be calculated from basic column-strength criteria. (T. Y. Galambos, Structural Stability Research Council Guide to Design Criteria for Metal Structures, John Wiley & Sons, Inc., New York.) In general, the buckling stress is considered equal to the yield stress at a slenderness ratio L/ r of zero and decreases to the classical Euler value with increasing L/ r.
Relative price-strength ratios for A572 grade 50 and other steels, at L/ r values from zero to 120 are shown graphically in Fig. 1.3. As before, A36 steel is the base. Therefore, ratios less than 1.00 indicate a material cost lower than that of A36 steel. The figure shows that for L/ r from zero to about 100, A572 grade 50 steel is more economical than A36 steel.
Thus the former is frequently used for columns in building construction, particularly in the lower stories, where slenderness ratios are smaller than in the upper stories.