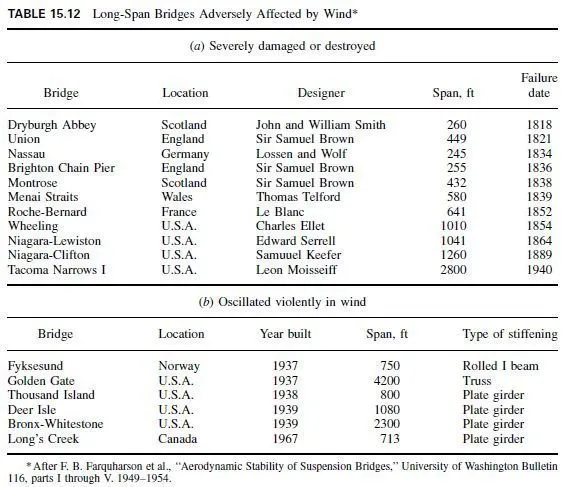
There are many types of dynamic loads. Periodic loads vary cyclically with time. Nonperiodic loads do not have a specific pattern of variation with time. Impulsive dynamic loading is independent of the motion of the structure. Impactive dynamic loading includes the interaction of all external and internal forces and thus depends on the motions of the structure and of the applied load.
To define a loading within the context of a dynamic or transient analysis, one must specify the direction and magnitude of the loading at every instant of time. The loading may come from either time-dependent forces being applied directly to the structure or from timedependent motion of the structures supports, such as a steel frame subjected to earthquake loading.
The term response is often used to describe the effects of dynamic loads on structures.
More specifically, a response to dynamic loads may represent the displacement, velocity, or acceleration at any point within a structure over a duration of time.
A reciprocating or oscillating motion of a body is called vibration. If vibration takes place in the absence of external forces but is accompanied by external or internal frictional forces, or both, it is damped free vibration. When frictional forces are also absent, the motion is undamped free vibration. If a disturbing force acts on a structure, the resulting motion is forced vibration (see also Art. 3.53).
In Art. 3.36, the concept of a degree of freedom is introduced. Similarly, in the context of dynamics, a structure will have n degrees of freedom if n displacement components are required to define the deformation of the structure at any time. For example, a mass M attached to a spring with a negligible mass compared with M represents a one-degree-offreedom system (Fig. 99a). A two-mass system interconnected by weightless springs (Fig. 3.99b) represents a two-degree-of-freedom system. The beam with the uniformly distributed mass in Fig. 3.99c has an infinite number of degrees of freedom because an infinite number of displacement components are required to completely describe its deformation at any instant of time.
Because the behavior of a structure under dynamic loading is usually complex, corresponding analyses are generally performed on idealized representations of the structure. In such cases, it is often convenient to represent a structure by one or more dimensionless weights interconnected to each other and to fixed points by weightless springs. For example, the dynamic behavior of the beam shown in Fig. 3.99c may be approximated by lumping its distributed mass into several concentrated masses along the beam. These masses would then be joined by members that have bending stiffness but no mass. Such a representation is often called an equivalent lumped-mass model. Figure 3.99d shows an equivalent fourdegree- of-freedom, lumped-mass model of the beam shown in Fig. 3.99c (see also Art. 3.53).